MATH

岡潔　”数学は必ず発見の前に一度行き詰まるのです．行き詰まるから発見するのです”

〇関数とグラフについて

ポイント

☆各象限について

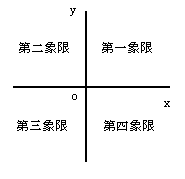
☆平行移動と対称移動

(※点についてはグラフにとれば明らかにわかるので，省略します．)

一般的に\(y=f(x)\)を平行移動するとき，\(x\)軸方向に\(p\)，\(y\)軸方向に\(q\)移動させた関数は\((y-q)=f(x-p) ⇔ y=f(x-p)+q\)

グラフを描いてみればなんとなくわかる．

例：\(y=5x+2\)の時，\(x\)軸方向に3，\(y\)軸方向に4移動させた関数は\(y−4=5(x−3)\)⇔\(y=5x−11\)

また対称移動についても，一般的に\(x\)軸対称は\(y=-f(x)\)，\(y\)軸対称は\(y=f(-x)\)，原点対称は\(-y=f(-x)\)⇔\(y=-f(-x)\)

例:\(y=5x+2\)の時，\(x\)軸対称は\(−y=5x+2⇔y=−5x−2\)，\(y\)軸対称は\(y=5(−x)+2=−5x+2\)，原点対称は\(−y=5(−x)+2⇔y=5x−2\)

☆一次関数について

定義域→\(x\)の範囲，値域→\(y\)の範囲

例：\(f(x)=3x+1\)で定義域が\((−2≦x≦4)\)のとき，\(f(0)=3\cdot 0+1=1\)，\(f(-1)=3\cdot(-1)+1=-2\)，\(f(3a+1)=3(3a+1)+1=9a+4\) \((−1≦a≦1)\)

最大値は\(x=4\)で\(y=13\)，最小値は\(x=−2\)で\(y=−5\)，つまり値域は\(−5≦y≦13\)

☆二次関数とは，\(y=ax^{2}+bx+c\)で表せる関数

例：\(y=2x^{2}+3x+1\)，\(y=-x^{2}，y=x^{2}+4\)

☆二次関数のグラフ

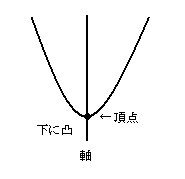
１，\(y=3x^{2}\)は軸が\(y\)軸．頂点は原点．下に凸．

２，\(y=2x^{2}+3\)は軸が\(y\)軸．頂点は\((0,3)\)．上に凸．(\(y=-2x^{2}\)のグラフを\(y\)軸方向に＋3だけ平行移動)

３，\(y=4(x-1)^{2}\)は軸が\(x=1\)．頂点は\((1,0)\)．下に凸．(\(y=4x^{2}\)のグラフを\(x\)軸方向に＋1だけ平行移動(※\(x\)は見た目マイナスに見えるが＋である！)

４，\(y=(x-3)^{2}+1\)は軸が\(x=3\)．頂点は\((3,1)\)．下に凸．(\(y=x^{2}\)のグラフを\(x\)軸方向に＋3，\(y\)軸方向に＋1だけ平行移動)

☆二次関数の変形(平方完成)

\(y=x^{2}+4x+1\)

\((x^{2}+2\cdot 2x)+1\)

\((~)^{2}\)の形を作ること！

\(=(x+2)^{2}-3\)

グラフでいうと軸は\(x=-2\)．頂点は\((−2,−3)\)．下に凸．

\(y=-3x^{2}+4x+2\)

\(=-3\left(x^{2}-2\displaystyle \cdot\frac{2}{3}x\right)\)

\(=-3\left(x^{2}-2\displaystyle \cdot\frac{2}{3}x+\displaystyle \frac{2^{2}}{3^{2}}\right)+\frac{2^{2}}{3}+2\)←－3はかっこの外側！

\(-3\left(x-\displaystyle \frac{2}{3}\right)^{2}+\displaystyle \frac{10}{3}\)

グラフで言うと軸は\(x=\displaystyle \frac{2}{3}\)．頂点は\(\left(\displaystyle \frac{2}{3},\frac{10}{3}\right)\)．上に凸．

☆二次関数のグラフと最大値・最小値

例　 \(f(x)=2x^{2}+3x+1\)で定義域が\((−2≦x≦4)\)のとき，

①式を平方完成する．

\(f(x)=2\left(x^{2}+2\displaystyle \cdot\frac{3}{4}x\right)+1=2\left(\displaystyle x^{2}+\frac{3}{4}x+\frac{9}{16}\right)-\displaystyle \frac{9}{8}+1=2\left(\displaystyle x+\frac{3}{4}\right)^{2}-\displaystyle \frac{1}{8}\)

ここでグラフをかいてみる．定義域をグラフに描けば最大値・最小値は明らか．

最大値は\(x=4\)で\(y=45\)，最小値は\(-\displaystyle \frac{3}{4}\)でy=\(-\displaystyle \frac{1}{8}\)，つまり値域は\(-\displaystyle \frac{1}{8}≦y≦45\)

※補足　連立3元1次方程式

問い

\(a+b+c=5\)…①

\(2a+3b+c=15\)…② から\(a,b,c\)を求めよ．

\(3a−b+2c=5\)…③

この問題を解く時は一つの文字を消して2つの文字だけにする．あとは2元１次連立方程式を解くだけ．

解答

②−２×①から　　\(b−c=5\)…④

③−３×①から　　\(−4b−c=−10\)…⑤

④−⑤から　　\(5b=15⇔b=3\)

④から　\(c=−2\)

①から　\(a=4\)

よって　\((a,b,c)=(4,3,−2)\)

☆二次関数の決定

１，頂点が\((3,2)\)で点\((2,1)\)を通る二次関数は，頂点から\(y=a(x-3)^{2}+2\)とおけるので，点を代入して求めると\(a=-1\)．よって\(y=-(x-3)^{2}+2=-x^{2}+6x-7\)

２，軸が\(x=4\)で二点\((3,5),(6,8)\)を通る二次関数は，軸から\(y=a(x-4)^{2}+b\)とおけるので，点を代入して整理すると，\(a+b=5\)，\(4a+b=8\)．連立方程式を解けば，\((a,b)=(1,4)\)．よって二次関数は，\(y=(x-4)^{2}+4=x^{2}-8x+20\)

３，3点\((−1,1)(2,−6)(3,9)\)を通る二次関数は，まず\(y=ax^{2}+bx+c\)とおくと，\(a-b+c=1\)，\(4a-2b+c=-6\)，\(9a+3b+c=9\)．これから\((a,b,c)=(−1,4,6)\)

よって二次関数は，\(y=-x^{2}+4x+6\)

４，3点\((−1,0)(3,0)(5,4)\)を通る二次関数は，まず\((−1,0),(3,0)\)から\(y=a(x+1)(x-3)\)とおけるので，点\((5,4)\)を代入して求めると，\(a=\displaystyle \frac{1}{3}\)．よって\(y=\displaystyle \frac{1}{3}(x+1)(x-3)\)

☆二次関数の応用

今長さ10のひもがある．このひもで長方形をつくるとき，面積が最大になるときの面積を求めよ．

作られた長方形の面積を\(S\)として一辺の長さを\(x\)とすると，\(x\)の範囲は(定義域)　\(0<x<5\)となる．この定義域のもとで面積Sは

\(S=x(5−x)=-x^{2}+5x=-\left(x-\displaystyle \frac{5}{2}\right)^{2}+\displaystyle \frac{25}{4}\)

これより最大値は\(\displaystyle \frac{5}{2}\)のときで\(\displaystyle \frac{25}{4}\)

問：\(f(x)=2x-3\)のとき，

\(f(0)，f(2)，f(2k+1)\)の値を求めよ．

\(f(0)=-3，f(2)=1，f(2k+1)=4k-1\)

¶二次不等式

ここは今後のために非常に重要なものになっていきます．基本的に二次関数と考えは変わりません．だいたいグラフの概形がかける程度でも大丈夫です．

○二次不等式

\(x^{2}-3x+2>0\)のように，二次式の不等式のことを二次不等式という．

例

\(x^{2}-3x+2>0\)を解く．まず，\(x^{2}-3x+2=(x-1)(x-2)\)となる．グラフを考えると，\(y\)が正の部分になっているのは，\(x<1，x>2\)である．

\(-x^{2}+4x-3\geqq 0\)を解く．まず，両辺に−1をかけて\(x^{2}-4x+3\leqq 0\)とする．\(x^{2}-4x+3=(x-1)(x-3)\)となる．グラフを考えると，\(y\)が負もしくは0の部分になっているのは，\(1≦x≦3\)である．

\(x^{2}+4x+4>0\)を解く．まず，\(x^{2}+4x+4=(x+2)^{2}\)である．グラフを考えると，\(y\)が正の部分となっているのは，\(x<−2，x>−2\)である．

\(x^{2}-6x+9\leqq 0\)を解く．まず，\(x^{2}-6x+9=(x-3)^{2}\)である．グラフを考えると，\(y\)が負もしくは0の部分になっているのは，\(x=3\)のみである．

\(x^{2}+3x+3\geqq 0\)を解く．\(x^{2}+3x+3=0\)において判別式\(D=−3\)となるので，\(x\)軸との共有点はない．グラフを考えると，\(y\)が正の部分となるのはすべての\(x\)である．

\(x^{2}+2x+4<0\)を解く．\(x^{2}+2x+4=0\)において判別式\(D=−12\)となるので，\(x\)軸との共有点はない．グラフを考えると，\(y\)が負の部分となるのは存在しない．

以上により，一般的には次のようになる．

\(y=ax^{2}+bx+c\)において，

①\(D>0\)のとき，

実数解を\(\alpha,\beta~(\alpha<\beta)\)をすると，

\(y≧0\)となるのは，\(x≦\alpha,x≧\beta\)

\(y>0\)となるのは，\(x<\alpha,x>\beta\)

\(y≦0\)となるのは，\(\alpha≦x≦\beta\)

\(y<0\)となるのは，\(\alpha<x<\beta\)

②\(D=0\)のとき，

実数解を\(\alpha\)(重解)とすると，

\(y≧0\)となるのは，全ての実数

\(y>0\)となるのは，\(\alpha\)以外のすべての実数\((x<\alpha,x>\alpha)\)

\(y≦0\)となるのは，\(x=\alpha\)

\(y<0\)となるのは，解はない

③\(D<0\)のとき，

\(y≧0\)となるのは，全ての実数

\(y>0\)となるのは，全ての実数

\(y≦0\)となるのは，解はない

\(y<0\)となるのは，解はない

○二次関数のグラフの位置関係と判別式

二次関数\(y=ax^{2}+bx+c\)と\(x\)軸との位置関係において，\(y=0\)の場合を考えればよいので，\(ax^{2}+bx+c=0\)において\(x\)の解は

\(x=\displaystyle \frac{-b\pm\sqrt{b^{2}-4ac}}{2a}\)なので，\(D=b^{2}-4ac\)の値によって実数解の数は変わってくる．

①\(D>0\)のとき，

異なる実数解を2つ持つ．よって\(x\)軸との共有点は2つとなる．

②\(D=0\)のとき，

実数解を1つ持つ(重解)．よって\(x\)軸との共有点は1つとなる．(接する)

③\(D<0\)のとき，

実数解は存在しない．よって\(x\)軸との共有点はない．

例題

\(y=x^{2}+2x+a\)と\(x\)軸との共有点の数を求めよ．

判別式\(\displaystyle \frac{D}{4}=1−a\)

よって

\(a>1\)のとき，共有点の数は0つ

\(a=1\)のとき，共有点の数は1つ

\(a<1\)のとき，共有点の数は2つ

別解

\(y=(x+1)^{2}+a-1\)からも求められる．

またx軸との共有点だけでなく，直線との共有点についても求められる．

例題

\(y=-x^{2}\)と\(y=4x+k\)が接するとき，\(k\)の値を求めよ．

連立方程式をたてると，

\(x^{2}+4x+k=0\)

判別式\(\displaystyle \frac{D}{4}=4-k\)

接するときは\(D=0\)なので，求める答えは\(k=4\)となる．

応用例題

\(y=ax^{2}-3x+a-4\)のグラフが\(x\)軸とを共有点を持たない時\(a\)の値の範囲を求めよ．

解答

※二次関数の場合にしか判別式\(D\)は使えない．

\(a\neq0\)のとき，

\(D=-4a^{2}+16a+9=-(2a+1)(2a-9)\)から，条件は\(D<0\)より，

\(-\displaystyle \frac{1}{2}<a<0,0<a<\frac{9}{2}\)となる．

\(a=0\)のとき，\(y=−3x−4\)となり，\(x\)軸と共有点を持つので不適．

○連立不等式

\(x^{2}-4x+3>0\)，\(x^{2}-5x\leqq 0\)の連立不等式を解け．

\(x^{2}-4x+3>0⇔(x-1)(x-3)>0⇔x<1,x>3\)

\(x^{2}-5x\leqq 0\) ⇔ \(x(x-5)\leqq 0\) ⇔ \(0\leqq x\leqq 5\)

よってこの範囲の共通部分を求めればよいので，

\(0\leqq x<1,~3<x\leqq 5\)