上級者
上級者
問題：\(xy\)平面上の楕円\(\displaystyle E:\frac{x^2}{3}+y^2=1\)上に3点\(P,Q,R\)をとる時，三角形\(PQR\)が正三角形になるという．正三角形の長さを\(a\)，重心\(G\)の座標を\((s,t)\)と置くときに次の問いに答えよ．(1)\(GP\)と\(x\)軸のなす角度を\(\theta\)（\(0\leqq \theta <2\pi\)）と置くとき，\(a,s,t\)と\(\theta\)の関係を求めよ．(2)\(P(0,1)\)の時，正三角形の長さおよび重心\(G\)の座標を求めよ．
難度: 5
問題：\(m,n\)を自然数とする．\(x \geqq 0\),\(y \geqq 0\)の場合で，曲線\(x^\frac{1}{m}+y^\frac{1}{n}=1\)と\(x\)軸，\(y\)軸とで囲まれる領域の面積を\(S(m,n)\)とする．(1)\(S(m,n+1)=\frac{n+1}{m+1}S(m+1,n)\)となることを示せ．(2)\(S(m,n)\)を\(m,n\)を用いて表せ．(3)\(\lim_{n\rightarrow \infty}(S(n,n))^\frac{1}{n}\)の値を求めよ．
難度: 4
(1)\(m,n\)を自然数とする．\(8^3+m^3=9^3-n^3\)を満たす時，\(m,n\)を求めよ．(2)\(m,n\)を自然数とする．\(12^3-m^3=n^3-1^3\)を満たす時，\(m,n\)を求めよ．
難度: 3
問題：\(P(x)=ax^3+bx^2+cx+d\)において，\(a\neq 0\)，\(P(a)=0\)，\(P(b)=0\)，\(P(c)=0\)となる時，(A)\(d=0\)の時，\(a,b,c\)を求めよ．(B)\(a,b,c,d\)が実数で，\(a>0\)の時，\(a\)の取りうる範囲を求めよ．
難度: 4
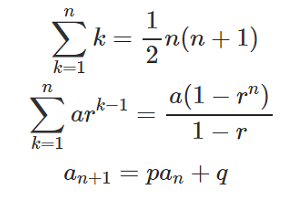
問題：\(△ABC\)において，\(BC,CA,AB\)の長さを\(a,b,c\)とする．いずれかの辺の中点を\(D\)とすると，その辺と対角にある三角形の頂点と\(D\)をつないだ線の長さを\(d\)とする時，\(a,b,c,d\)が等比数列になる．\(a=1\)とする．考えられる\(△ABC\)の中で最小の面積を求めよ．
難度: 4
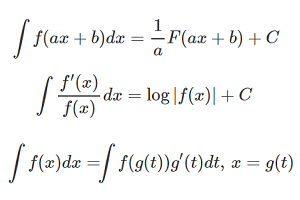
問題：\(\lim_{N\rightarrow \infty}\int_{0}^{N} \frac{1}{1+x^2}dx=\frac{\pi}{2}\)を用いて，次の積分値を求めよ．(A)\(I=\lim_{n\rightarrow \frac{\pi}{4}-0}\int_{0}^{n} \frac{1}{\sin^4 x+\cos^4 x}dx\)(B)\(I=\lim_{n\rightarrow \frac{\pi}{4}-0}\int_{0}^{n} \frac{1}{\sin^6 x+\cos^6 x}dx\)
難度: 4
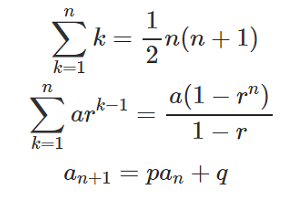
問題：実数\(x\)，整数\(n\)に対し，\(n\leqq x<n+1\)を満たす場合に\([x]=n\)と表す．正の整数\(k\)に対して，\(a_{k}\)\(=[\sqrt{k}]\)とする時，\(\sum_{k=1}^{2020}a_{k}\)を求めよ．
難度: 3
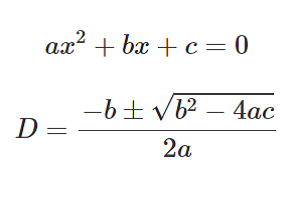
問題：(1)\(n\)を自然数とする．\(x^{2n}+x^n+1\)を係数が実数の範囲で因数分解しなさい．(2)\(x^{10}+x^{5}+1\)を係数が整数の範囲で因数分解しなさい．
難度: 5
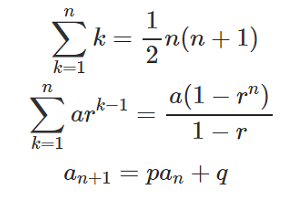
問題：数列\(a_{n}\)は\(a_{1}=1\)，\(a_{2}=2\)，\(a_{3}=3\)，\(a_{n}a_{n+3}-a_{n+1}a_{n+2}\)\(=-2(a_{n+1}^2-a_{n}a_{n+2})\)を満たす時，この数列の一般項\(a_{n}\)を求めよ．
難度: 3
問題：\(a,b\)を実数とする．\(n\)を自然数とする場合に，\(a^2+b^2=3\)，\(a^4+b^4=7\)，\(a^{n}+b^{n}\)\(<a^{n+1}+b^{n+1}\)が成立する時，\(a^{n}+b^{n}\)\(+a^{n+1}+b^{n+1}\)\(=a^{n+2}+b^{n+2}\)が成立することを示せ．
難度: 4
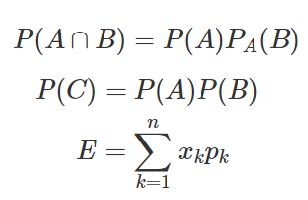
問題：サイコロを\(n\)回投げる．全ての目の出る確率が同様に確からしい場合，次の問いに答えよ．(1)出た目の和が7の倍数となる確率を求めよ． (2)出た目の和が\(n\)回目で初めて6の倍数となる確率を求めよ．(3)出た目の和が5の倍数となる確率を求めよ．
難度: 5
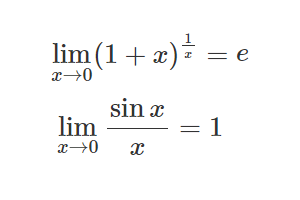
問題：(1)数列\({a_{n}}\)は，\(a_{n}>0\)，\(a_{n+1}^2=a_{n}+12\)（\(n=1,2,\cdots\)）を満たすとする．この時，極限\(\lim_{n\rightarrow \infty}a_{n}\)を求めよ．(2)数列\({a_{n}}\)は，\(a_{n}>0\)，\(a_{n+1}^2\)\(=na_{n}+2n^2+3n+1\)（\(n=1,2,\cdots\)）を満たすとする．この時，極限\(\lim_{n\rightarrow \infty}\frac{a_{n}}{n}\)を求めよ．
難度: 3
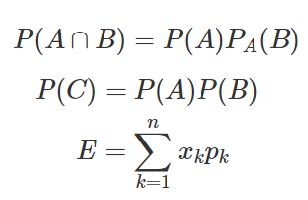
問題：あるコンピュータプログラムを使い，仮想的に\(A,B\)2人でじゃんけんを行う．なお，コンピュータの設定でじゃんけんのグー・チョキ・パーの出す確率を変えられるとする．①じゃんけんの設定で\(A,B\)のグー・チョキ・パーの出す確率を同じとする場合，2回じゃんけんした時の\(A\)が勝ち越す確率\(P_{A}\)の範囲を求めよ．②\(n\)回じゃんけんした時に全て勝ち続けるか，あいこになり続けるか，負け続ける場合の確率\(X\)の範囲を求めよ．
難度: 4
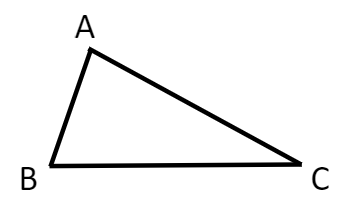
問題：一辺の長さが1の正三角形\(ABC\)において，\(AB\)上に点\(D\)，\(AC\)上に点\(E\)を取り，\(DE\)で折り曲げる．三角形の重なった面積を\(S\)とする．\(AD=x\),\(AE=y\)とする時，面積を\(x,y\)で表せ．
難度: 5
問題：三角形\(ABC\)において，\(A\)が\(y\)軸上にあり，\(BC\)が\(x\)軸上にあり，\(BC\)の中点が原点にある．また\(AB,AC\)が，原点を中心とする半径1の円に接している．(1)三角形\(ABC\)の面積の最小値を求めよ．(2)三角形\(ABC\)の辺の長さの最小値を求めよ．
難度: 4
問題：\(a,b,c\)を実数とする三次関数\(f(x)=x^3+ax^2+bx+c\)において，\(f(x)=0\)が3つの実数解を持つとする．極大値となる\(x\)を\(m\)，極小値となる\(x\)を\(n\)とするとき，①3つの実数解の範囲を\(m,n\)を使って求めよ．②\(mn=-1\)を満たし，①で求めた実数解の範囲の最大値，最小値が\(f(x)=0\)の時，\(x\)軸と\(f(x)\)で囲まれる面積\(S\)の最小値を求めよ．
難度: 4
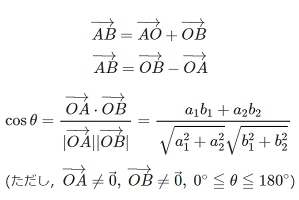
問題：三角形\(ABC\)において，\(BC=a\)，\(CA=b\)，\(AB=c\)，\(\displaystyle \overrightarrow{AB}\cdot\overrightarrow{AC}=p\)，\(\displaystyle \overrightarrow{BA}\cdot\overrightarrow{BC}=q\)，\(\displaystyle \overrightarrow{CA}\cdot\overrightarrow{CB}=r\)とした時に次の問いに答えよ．(i)三角形\(ABC\)の各辺の長さは整数，\(p\)は素数，\(r=k^2\)，\(k\)は正の整数の時，\(p\)が最小となる時の\(p,q,r\)を求めよ．(ii)\(4(p^2+q^2+r^2)\)\(\geqq a^4+b^4+c^4\)が成立することを示せ．また，等号成立する場合の\(a,b,c\)の条件を求めよ．
難度: 3
問題：\(m,n,r,s\)を正の整数とする．\({}_{r}P_{s}+{}_{r}C_{s}=m!+n!\)が成立し，\(m,n,r,s\)を小さい順に並べた数列が公差1の等差数列である時，\(m,n,r,s\)を求めよ．
難度: 6
問題：各辺が\(a,b,c\)の三角形\(ABC\)において，\(a+c=2b\)が成り立ち，三角形\(ABC\)のある角度が\(60^{\circ}\)の時，三角形\(ABC\)は正三角形になることを示せ．
難度: 3
問題：一次関数\(y=ax+b\cdots(1)\)，二次関数\(y=ax^2+bx+c\cdots(2)\)，三次関数\(y=ax^3+bx^2+cx\cdots(3)\)でいずれの関数の組み合わせでも実数の重解を持つ場合，一次関数と三次関数で囲まれる面積を\(S_{1}\)，二次関数と三次関数で囲まれる面積を\(S_{2}\)とした時，\(S_{1}/S_{2}\)の値を求めよ．
難度: 6
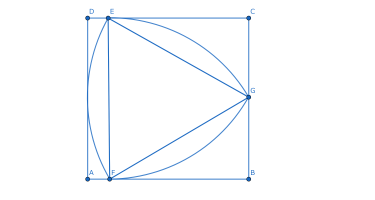
問題：一辺が\(a\)の正方形\(ABCD\)の中に，一辺が\(a\)の正三角形\(EFG\)の各頂点を中心に，異なる二頂点を半径\(a\)の円弧で結んでできる図形であるルーローの三角形が存在する．このルーロの三角形は，常に頂点か円弧が正方形\(ABCD\)の辺に接しながら，正方形\(ABCD\)の内部を動いている．この場合，ルーローの三角形が動く範囲の面積を求めよ．
難度: 5
問題：一辺の長さが\(s\)の正三角形の重心が原点にあり，原点中心で三角形が回転する．ある放物線が三角形の全ての頂点を通る時に，放物線と三角形で囲まれる部分で，正三角形の面積を除く部分の面積の最小値を求めよ．
難度: 5
問題：\(x^{4}+ax^{3}+bx^{2}+cx=0\)の解を\(\alpha\),\(\beta\),\(\gamma\),\(0\)とすると，\(\frac{1}{\alpha+\beta+\gamma}=\frac{1}{\alpha\beta}+\frac{1}{\beta\gamma}+\frac{1}{\gamma\alpha}\)\(=\frac{1}{\alpha}+\frac{1}{\beta}+\frac{1}{\gamma}\)が成り立っている．① \(f(x)=x^{4}+ax^{3}+bx^{2}+cx\)と置く．\(f(x)=0\)が異なる3つの実数解を持つ時，\(f(x)\)を求めよ．③ ①のとき\(n\)を整数とする時，\(f(n)\)は12で割ると余りが6か0になることを示せ．また余りが6になるときを\(n\)の値が小さい順から\(k_{1},k_{2},\cdots\)とするとき，数列\(k_{i}\)を求めよ．
難度: 2,5
問題：以下の式を満たす素数\(p,q\)を求めよ． (1) \(\displaystyle \sum_{k=1}^{n}k^2=p\) (2) \(\displaystyle \sum_{k=1}^{n}k^2=pq\) \((p<q)\)
難度: 4
問題：\(\displaystyle f(n)=\frac{1}{4}n^{4}+an^{3}+bn^{2}+cn+d\)とおく．定数\(a,b,c,d\)は\(\displaystyle 0 \leqq a<\frac{1}{2}\)，\(\displaystyle 0 \leqq b<\frac{1}{2}\)，\(\displaystyle 0 \leqq c<\frac{1}{2}\)，\(\displaystyle 0 \leqq d<\frac{1}{2}\)を満たし，すべての整数\(n\)に対して\(f(n)\)は整数である．この条件を満たす\((a,b,c,d)\)の組をすべて求めよ．
難度: 4
問題：放物線\(y=ax^{2}+bx+c\)が2直線\(y=sx+u\)，\(y=tx+u\)と接する場合，その接点の\(x\)座標の和が0であることを示せ．ただし\(s \neq t\)である．
難度: 3
問題：今放物線\(z=y^{2}\)を\(z\)軸の周りの回転して得られる曲面を\(A\)とする．またこれを\(z=y+2\)となる平面\(B\)で切る．このとき，（１）曲面\(A\)と平面\(B\)に囲まれる体積を求めよ．（２）切り口上に光源点\(P\)をとる．点\(P\)がこの切り口上を動くとき，\(z=0\)の\(xy\)平面で影となる部分の面積を求めよ．
難度: 6
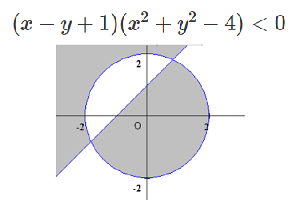
問題：実数\(x,y\)が\(4x^2y^2+2xy+x^2+y^2\leqq 3\)を満たしながら変化するとする．\(m>0\)の時，\(xy-m(x+y)\)の最大値を\(m\)を用いて表せ．
難度: 4
問題：1辺の長さが\(1,1,\sqrt{2}\)の直角二等辺三角形を底面とし高さが1の三角柱を考える．この三角柱を平面で切り，その断面が3辺とも三角柱の側面上にある正三角形であるようにする．そのような正三角形の面積がとりうるような値の範囲を求めよ．
難度: 3
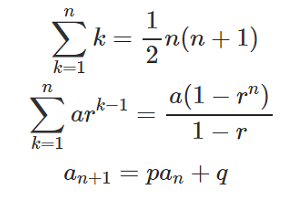
問題：(1) \(a_{1}=1\)，\(\frac{a_{1}+2a_{2}+\cdots+na_{n}}{n}=a_{n+1}\)で，数列\(a_{n}\)の一般項を求めよ．(2) \(\lim_{n\rightarrow\infty}(a_{n})^{\frac{1}{n}}\)を求めよ．
難度: 3
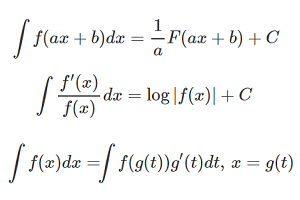
問題：(1)\(x=\frac{1}{\sqrt{3}}\sin t+\cos t\)，\(y=\frac{1}{\sqrt{3}}\sin t-\cos t\) \((0\leqq t<2\pi)\)の概形を\(xy\)平面に描け．(2)\(x\)軸で図形を回転させた時にできる立体の体積を求めよ．
難度: 3
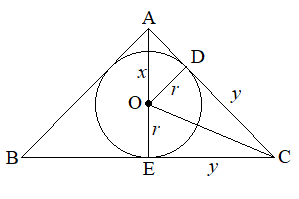
問題：二等辺三角形の中に半径\(r\)の内接円が存在する．(1)二等辺三角形の面積が最小となる時，三角形の面積を\(r\)を用いて表せ．(2)二等辺三角形の辺の長さが最小となる時，辺の長さを\(r\)を用いて表せ．
難度: 4
問題：数列\({a_n}\)（\(n\)は自然数）において，\(a_n>0,a_1>1\)，\(\displaystyle \frac{a_n^3}{a_n^2+1}=\frac{1}{2}a_{n+1}^2\)が成立するとき，\(1<a_n<a_{n-1}<\cdots<a_1\)が成立することを示せ．
難度: 4
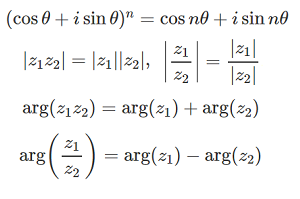
問題：②，他3問：\(1+\cos\theta+\cdots+\cos n\theta=\frac{\cos\frac{n\theta}{2}\sin\frac{(n+1)\theta}{2}}{\sin\frac{\theta}{2}}\)，\(\sin\theta+\cdots+\sin n\theta=\frac{\sin\frac{n\theta}{2}\sin\frac{(n+1)\theta}{2}}{\sin\frac{\theta}{2}}\)が成立することを示せ．
難度: 5
問題：放物線\(y=\frac{1}{2}x^{2}\)上に点\(A\),点\(B\)が存在する．点\(A\),点\(B\)の接線同士が直交する時に，距離\(AB\)が最小となる時の距離を求めよ．
難度: 4
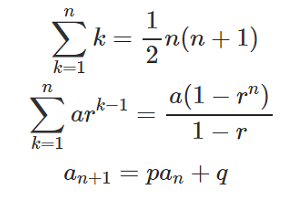
問題：\(a_{n+2}=a_{n+1}+a_{n}\)，\(a_{1}=1\)，\(a_{2}=1\)のとき次のことを示せ．(1) \(n\)は4の倍数 \(\Leftrightarrow\) \(a_{n}\)は3の倍数 (2) \(a_{n}=n^{2}\)が成り立つとき，\(n\)を求めよ．（その他複数問）
難度: 4
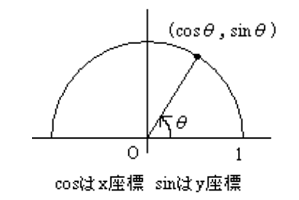
問題：(1)\(0\leqq x <\pi\)の時，\(\tan x\tan 2x \tan 3x\)\(=\tan x+\tan 2x+\tan 3x\)を解け．(2)\(a+b+c=\pi\)の時，\(\tan a+\tan b+\tan c\)\(=\tan a \tan b \tan c\)であることを示せ． (3)\(\sin 10^{\circ}\sin 30^{\circ}\sin 50^{\circ}\sin 70^{\circ}\)\(=\frac{1}{16}\)であることを示せ． (4)\(\cos 0^{\circ}\cos 20^{\circ}\cos 40^{\circ}\cos 60^{\circ}\cos 80^{\circ}\)を求めよ．
難度: 3
問題：放物線\(y=x^2\)から接線を2本引く．放物線と接線に囲まれる面積を\(S\)，各接点と接線同士の交点までの距離を\(d_{1}\)，\(d_{2}\)とする．2つの接点を通る直線が放物線の焦点\((0,\frac{1}{4})\)を通るとき，\(\frac{S}{d_{1}d_{2}}\)が一定であることを示せ．
難度: 4
問題：\(a_{1}\geqq a_{2}\geqq\cdots\geqq a_{n}\)，\(b_{1}\geqq b_{2}\geqq\cdots\geqq b_{n}\)のとき，\(\displaystyle \frac{1}{n}\sum_{k=1}^{n}a_{k}b_{k}\)\(\displaystyle \geqq(\frac{1}{n}\sum_{k=1}^{n}a_{k})(\frac{1}{n}\sum_{k=1}^{n}b_{k})\)となることを示せ．
難度: 4
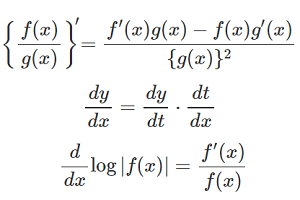
問題：(1) \(0 \leqq x <\pi\)の時，\(-16\tan 2x+45\tan x=3\)を満たす\(\tan x\)を求めよ．(2) \(0 \leqq x <\pi\)の時，\(a\tan 2x+45\tan x=3\)（\(a\)は定数）を満たす\(x\)の値はいくつか，\(a\)の値によって分類せよ．
難度: 4
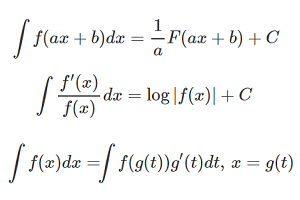
問題：半径6，高さ8の円柱を考える．今，上底面と下底面の円周上に点を取り，その点の距離が常に10となるように点が動くとする．その点と点を棒で結ぶ．点が円周上を動く時この棒が描く図形と円柱の上下の円が囲む図形の体積を求めよ．
難度: 5
問題：\(a,b,c\)は，\(a^{2}+b^{2}=c^{2}\)をみたす自然数とする（ピタゴラス数）．(1)\(a,b\)ののうち少なくとも片方は3の倍数となることを示せ．(2)\(a,b\)のうち少なくとも片方は4の倍数となることを示せ．(3)\(abc\)は60で割り切れることを示せ．
難度: 3
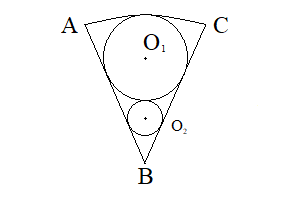
問題：図のように扇形の内部に円が順番に\(B\)に接近しながら接している．円\(O_{n}\)の半径を\(r_{n}\)とし，面積を\(S_{n}\)とする．また，扇形の面積\(T\)とする．このとき，\(\displaystyle \lim_{\angle ABC\rightarrow 0}\frac{\sum_{n=1}^{\infty}S_{n}}{T}\)を求めよ．
難度: 3
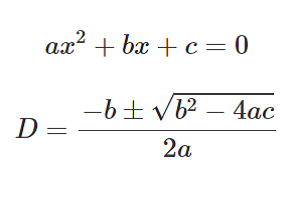
問題：\(a^{3}+b^{3}+c^{3}=81\cdots\)① \((a+b+c)^{3}=729\cdots\)② \(ab+bc+ca=x\cdots\)③ \(a,b,c\)が実数の解を持つときの\(x\)の範囲は？
難度: 4
問題：\([x]\)は\(x\)を超えない最大の整数を意味する．次の式を満たす\(x,y\)を求めよ． \(\displaystyle x+[y]=\frac{7}{5}\cdots\)① \(\displaystyle \left[\frac{1}{x}\right]+\frac{1}{y}=\frac{13}{5}\cdots\)②
難度: 3
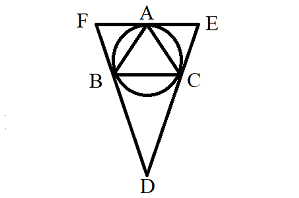
問題：\(AB=AC\)のとき，\(△DEF\)の面積を\(S'\)，\(△ABC\)の面積を\(S\)とすると，\(\displaystyle \frac{S'}{S}\)の範囲をあらわせ．
難度: 4
問題：(1)\(e^{\pi}\)と\(\pi^{e}\)はどちらが大きいか？ (2)\(a^{b}=b^{a}\)を満たすような自然数\(a,b\)を求めよ．(\(a\neq b\))
難度: 3
問題：次の方程式を\(x\)について解け．(A) \(\sqrt{2}\sin x +\sqrt{2}\cos x +\tan x =3\) \((0\leqq x<\pi)\) (B) \(\sqrt{2}\sin x +\sqrt{2}\cos x +\tan x =2\) \((0\leqq x<2\pi)\)
難度: 7
問題：\(n\)を自然数とするとき，次の和を求めよ．(A) \(\displaystyle \sum_{k=0}^{n} k {}_{n}C_{k}\)，(B) \(\displaystyle \sum_{k=0}^{n} k^{2} {}_{n}C_{k}\)，(C) \(\displaystyle \sum_{k=0}^{n} k^{3} {}_{n}C_{k}\)
難度: 4
問題：\(x,y\)が2つの不等式\(x \geqq y\cdots\)①，\(y\geqq x^{2}-3x+1\cdots\)②を満たすとき，\(\displaystyle \frac{x^{2}}{3x^{2}-4xy+2y^{2}}\)のとりうる値の最大値，最小値を求めよ．
難度: 3
問題：\(f(x)=x^3+ax^2+bx+p\)において，\(a,b\)が整数，\(p\)が素数とする．(1)\(a,b\)は\(b=ka\) \(\left(\displaystyle 1<k \leqq\frac{3}{2}\right)\)を満たすとする．\(f(x)=0\)がただ1つの解を持ち，それが整数解の時，\(a,b,p\)を求めよ．
難度: 5
問題：今，\(y=a^{3}x^{2}\)となるグラフに上から\(\displaystyle \frac{1}{a}\)の棒を落とす．このときに棒と放物線が囲む面積の最大値が\(a\)に無関係であることを求めよ．
難度: 4
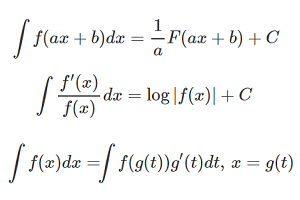
問題：定積分\(I=\displaystyle \int_{0}^{\pi}\frac{x\sin^{2}x}{\sin^{6}x+\cos^{6}x}dx\)の値を求めよ．なお，\(\displaystyle \int_{0}^{\frac{\pi}{2}}\frac{1}{\sin^{6}x+\cos^{6}x}dx\)\(=\pi\)であることを使ってもよい．
難度: 7
問題：\((a_{1}^{2}+a_{2}^{2}+\cdots+a_{n}^{2})(b_{1}^{2}+b_{2}^{2}+\cdots+b_{n}^{2})\)\(\geqq(a_{1}b_{1}+a_{2}b_{2}+\cdots+a_{n}b_{n})^{2}\)であることを数学的帰納法を用いて示せ．
難度: 3
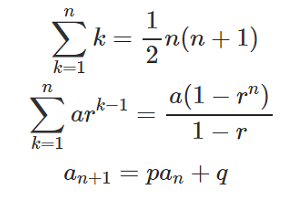
問題：\(\{a_{n}\}\)の初項\(a_{1}\)から第\(n\)項\(a_{n}\)までの和を\(S_{n}\)とする．\(a_{1}=-1,S_{n}S_{n-1}=a_{n}\)を満たす数列\(a_{n}\)を求めよ．
難度: 3
問題：\(a^{4}+4b^{4}=pq\)で，\(a,b\)は自然数，\(p,q\)は\(p<q\)となる素数の時，\(p\)が最小となる場合の\(a,b,p,q\)の値を求めよ．
難度: 5
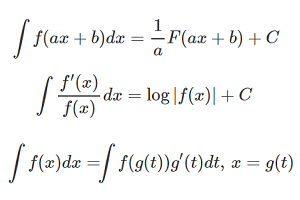
問題：(1)ガンマ関数は\(\displaystyle \Gamma(n)=\lim_{\alpha\rightarrow\infty}\int_{0}^{\alpha}t^{n-1}e^{-t}dt\)という式で表せる．次の式が成り立つことを証明せよ．\(\Gamma(n)=(n-1)!\)
難度: 6
問題：（１）\(n^{m}-n!=2\cdots①\)が成り立つ自然数\(m,n\)を求めよ．（２）\(p,q\)は\(q>p\)となる素数である時，\(n^{q}-n!=p\cdots②\)が成り立つ自然数\(n\)は存在しないことを示せ．
難度: 2,6