MATH

ユークリッド　”幾何学に王道なし”

☆三角比

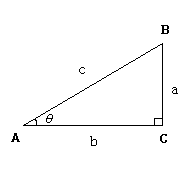
正接…tan（タンジェント）のこと．\(\displaystyle \tan\theta=\frac{a}{b}\) \((\displaystyle \tan 30°=\frac{1}{\sqrt{3}}，\tan 45°=1，\tan 60°=\sqrt{3})\)

正弦…sin（サイン）のこと．\(\displaystyle \sin\theta=\frac{a}{c}\) \((\displaystyle \sin 30°=\frac{1}{2}，\sin 45°=\frac{1}{\sqrt{2}}，\sin 60°=\frac{\sqrt{3}}{2})\)

余弦…cos（コサイン）のこと．\(\displaystyle \cos\theta=\frac{b}{c}\) \((\displaystyle \cos 30°=\frac{\sqrt{3}}{2}，\cos 45°=\frac{1}{\sqrt{2}}，\cos 60°=\frac{1}{2})\)

☆三角比の性質

今の時点では１～３までをしっかり覚えておきましょう．以下は三角関数でもやります．

１，\(\tan x=\displaystyle \frac{\sin x}{\cos x}\)

２，\(\sin^{2}x+\cos^{2}x=1\)

\(\rightarrow\)３，\(1+\tan^{2}x=\displaystyle \frac{1}{\cos^{2}x}\)(両辺を\(\cos^{2}x\)で割った．)

\(\sin(180°-x)=\sin x，\cos(180°-x)=-\cos x，\tan(180°-x)=-\tan x\)

\(\sin(90°-x)=\cos x，\cos(90°-x)=\sin x，\tan(90°-x)=\displaystyle \frac{1}{\tan x}\)

→\(\displaystyle \tan 150°=-\frac{1}{\sqrt{3}}\)，\(\tan 135°=-1\)，\(\tan 120°=-\sqrt{3}\)，\(\sin 150°=\displaystyle \frac{1}{2}\)，\(\sin 135°=\displaystyle \frac{1}{\sqrt{2}}\)，\(\sin 120°=\displaystyle \frac{\sqrt{3}}{2}\)，\(\cos 150°=-\displaystyle \frac{\sqrt{3}}{2}\)，\(\cos 135°=\displaystyle \frac{1}{\sqrt{2}}\)，\(\cos 120°=\displaystyle \frac{1}{2}\)

○拡張

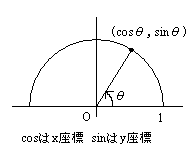
\(\cos\)は\(x\)座標,\(\sin\)は\(y\)座標と覚えよ．

\(0°≦\theta≦180°\)とする．円上だから\(0≦\sin x≦1,−1≦\cos x≦1\)

☆等式を満たす\(\theta\)，三角比の値

例　\(\displaystyle \sin\theta=\frac{1}{2}\)を満たす\(\theta\)を求めよ．

上の値を覚えていれば，\(\theta=30°,150°\)

例　\(0°≦x≦180°\)とする．\(\displaystyle \sin x=\frac{5}{13}\)のとき，\(\cos x,\tan x\)の値を求めよ．

\(\sin^{2}x+\cos^{2}x=1\)より，\(\cos^{2}x=\displaystyle \frac{144}{169}\)

\(0°≦x≦90°\)のとき，\(\cos x≧0\)より，

\(\cos x=\displaystyle \frac{12}{13}\) また，\(\tan x=\displaystyle \frac{\sin x}{\cos x}=\frac{5}{12}\)

\(90°≦x≦180°\)のとき，\(\cos x≦0\)より，

\(\cos x=-\displaystyle \frac{12}{13}\) また，\(\tan x=\displaystyle \frac{\sin x}{\cos x}=-\frac{5}{12}\)

☆直線の傾き

図のように直線の傾き=\(\tan\)となる．

☆正弦定理と余弦定理

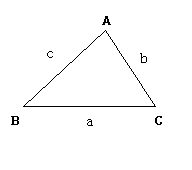
以下，図のように各辺をa,b,c，角度をA,B,Cとして公式を定義する．

○正弦定理

\(△ABC\)の外接円の半径を\(R\)とすると，

\(\displaystyle \frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}=2R\)

○余弦定理

\(a^{2}=b^{2}+c^{2}-2bc\cos A\) \(\left(\displaystyle \cos A=\frac{b^{2}+c^{2}-a^{2}}{2bc}\right)\)

\(b^{2}=c^{2}+a^{2}-2ca\cos B\) \(\left(\displaystyle \cos B=\frac{c^{2}+a^{2}-b^{2}}{2ca}\right)\)

\(c^{2}=a^{2}+b^{2}-2ab\cos C\) \(\left(\displaystyle \cos C=\frac{a^{2}+b^{2}-c^{2}}{2ab}\right)\)

証明は教科書に書いてあるの思うので，見てください．証明はできなくてもいいと思います．

例題

\(△ABC\)において\(b=\sqrt{6},c=1+\sqrt{3},A=45°\)のとき\(a,B,C\)を求めよ．

このような問題は正弦定理や余弦定理を使えば解けます．

余弦定理より\(a^{2}=b^{2}+c^{2}-2bc\cos A=4\)，\(∴a=2\)

次に正弦定理より，\(\displaystyle \frac{a}{\sin A}=\frac{b}{\sin B}\)⇔\(\displaystyle \frac{2}{\sin 45°}=\frac{\sqrt{6}}{\sin B}\) ⇔ \(\displaystyle \sin B=\frac{1}{2}\) ⇔ \(B=30°\)（\(150°\)はすべての角の合計が\(180°\)なのでない．）

また，\(C=180°－45°－30°=75°\)

例題

\(△ABC\)において\(a=\sqrt{3},b=1,B=30°\)のとき，\(c,A,C\)を求めよ．

正弦定理を使うタイミングは対応する辺と角，あと１辺もしくは角がわかる時です．（たとえば，\(A,a,b\)や\(A,B,b\)など）

また余弦定理を使うタイミングは2辺と1角が分かる時です．（たとえば，\(A,a,b\)や\(A,b,c\)など）

よってこの問題ははじめどちらを使ってもできます．

１，正弦定理にて，

正弦定理より，\(\displaystyle \frac{a}{\sin A}=\frac{b}{\sin B}\)⇔\(\displaystyle \frac{\sqrt{3}}{\sin A}=\frac{1}{\sin 30°}\)⇔\(\displaystyle \sin A=\frac{\sqrt{3}}{2}\)⇔\(A=60°\)また\(120°\)

\(A=60°\)のとき，\(C=90°\)

また正弦定理より，\(c=2\)

\(A=120°\)のとき，\(C=30°\)

また正弦定理より，\(c=1\)

2，余弦定理にて

余弦定理より，\(b^{2}=c^{2}+a^{2}-2ca\cos B\) ⇔ \(1=c^{2}+3-2\sqrt{3}c\cos 30°\) ⇔ \((c−1)(c−2)=0\)

\(c=1\)のとき，余弦定理では，\(\displaystyle \cos A=\frac{b^{2}+c^{2}-a^{2}}{2bc}\)から，\(A=120°\)．よって\(C=30°\)（もちろん正弦もOK）

\(c=2\)のとき，余弦定理では\(\displaystyle \cos A=\frac{b^{2}+c^{2}-a^{2}}{2bc}\)から，\(A=60°\)．よって\(C=90°\)

例題

\(△ABC\)において次の等式が成り立つとき，最小の角の余弦の値を求めよ．また\(b=\sqrt{7}\)のとき，外接円の半径を求めよ．

\(\displaystyle \frac{\sin A}{5}=\frac{\sin B}{4}=\frac{\sin C}{6}\)

余弦定理から，\(\displaystyle \sin A=\frac{a}{2R},~\sin B=\frac{b}{2R},~\sin C=\frac{c}{2R}\)．これを上の等式に代入して整理すると，

\(\displaystyle \frac{a}{5}=\frac{b}{4}=\frac{c}{6}\)．よって\(a=5k,~b=4k,~c=6k\)とおくと\(b\)が最も小さい辺なので，\(B\)が最小の角となる．

よって，\(\displaystyle \cos B=\frac{c^{2}+a^{2}-b^{2}}{2ca}=\frac{(6k)^{2}+(5k)^{2}-(4k)^{2}}{2\times 6k\times 5k}=\frac{3}{4}\)

また\(\sin^{2}B+\cos^{2}B=1\)から，\(\sin B=\displaystyle \frac{\sqrt{7}}{16}\)

よって正弦定理より，\(R=\displaystyle \frac{b}{2\sin B}=8\)

☆図形の計量

○三角形の面積

\(△ABC\)の面積を\(S\)とすると，

\(S=\displaystyle \frac{1}{2}bc\sin A=\frac{1}{2}ca\sin B=\frac{1}{2}ab\sin C\)

※ヘロンの公式（これは覚えなくてもよい．）余弦定理から求まる．

\(S=\sqrt{s(s-a)(s-b)(s-c)}\)．ただし，\(s=\displaystyle \frac{a+b+c}{2}\)

○球の体積\(V\)と表面積\(S\)（球の半径を\(r\)とする）

\(V=\displaystyle \frac{4}{3}\pi r^{3} S=4\pi r^{2}\)

○相似と計量

相似な図形では，対応する線分の長さの比，角の大きさは等しい．

また相似比が\(m:n\)であるとき，面積比は\(m^{2}:n^{2}\)，体積比は\(m^{3}:n^{3}\)である．