MATH

デカルト　”我思う，ゆえに我あり”

¶図形と方程式

☆点と直線

○平面上の距離・内分点・外分点

2点を\(A(x_{1},y_{1}),B(x_{2},y_{2})\)とする．

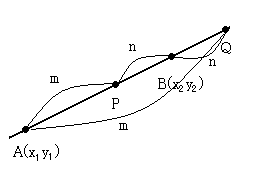
距離\(AB\)は\(AB=\sqrt{(x_{1}-x_{2})^{2}+(y_{1}-y_{2})^{2}}\)

線分\(AB\)を\(m：n\)に内分する点の座標は\(P\left(\displaystyle \frac{nx_{1}+mx_{2}}{m+n},\displaystyle \frac{ny_{1}+my_{2}}{m+n}\right)\)

特に中点の座標は\(\left(\displaystyle \frac{x_{1}+x_{2}}{2},\displaystyle \frac{y_{1}+y_{2}}{2}\right)\)

また，\(m：n\)に外分する点の座標は\(Q\left(\displaystyle \frac{-nx_{1}+mx_{2}}{m-n},\displaystyle \frac{-ny_{1}+my_{2}}{m-n}\right)\)

例　中線定理の証明

\(△ABC\)の辺\(BC\)の中点を\(M\)とする．このとき，\(AB^{2}+AC^{2}=2(AM^{2}+BM^{2})\)等式が成り立つことを示せ．

座標の取り方を工夫する．

\(M\)を原点とし，辺\(BC\)が\(x\)軸に乗るようにする．このとき，座標は\(A(a,b),B(−c,0),C(c,0)\)ととる．

\(AB^{2}+AC^{2}=(-c-a)^{2}+(-b)^{2}+(c-a)^{2}+(-b^{2})=2(a^{2}+b^{2}+c^{2})\)

\(AM^{2}=a^{2}+b^{2} BM^{2}=c^{2}\)

よって\(AB^{2}+AC^{2}=2(AM^{2}+BM^{2})\)が成り立つことが分かる．

○三角形の重心

3点\(A(x_{1},y_{1}),B(x_{2},y_{2}),C(x_{3},y_{3})\)を頂点とする\(△ABC\)の重心\(G\)の座標は\(\left(\displaystyle \frac{x_{1}+x_{2}+x_{3}}{3},\displaystyle \frac{y_{1}+y_{2}+y_{3}}{3}\right)\)

○直線の方程式

１，

点\((x_{1},y_{1})\)を通り，傾きが\(m\)の直線の方程式は，\(y-y_{1}=m(x-x_{1})\)

点\((x_{1},y_{1})\)を通り，\(x\)軸に垂直な直線の方程式は，\(x=x_{1}\)

点\((x_{1},y_{1})\)を通り，\(y\)軸に垂直な直線の方程式は，\(y=y_{1}\)

２，

異なる2点\(A(x_{1},y_{1}) B(x_{2},y_{2})\)を通る直線の方程式は

\(x_{1}\neq x_{2}\)のとき， \(y-y_{1}=\displaystyle \frac{y_{2}-y_{1}}{x_{2}-x_{1}}(x-x_{1})\)

\(x_{1}=x_{2}\)のとき， \(x=x_{1}\)

例

2点 \((1,3),(3,−1)\)を通る直線の方程式は

\(y=-2x+5\)

○2直線・直線と点の関係

2直線が平行⇔傾きが同じ ⇔ \(m_{1}=m_{2}\)

2直線が垂直⇔傾きの積が\(−1⇔m_{1}m_{2}=-1\)

2直線の関係として

1，1点で交わる

2，並行で交わらない

3，一致する

がある．それぞれについて直線どうしの連立方程式を解くことで求められる．この条件は

1，連立方程式でただ1つの解をもつ．

2，連立方程式は解をもたない．

3，連立方程式は無数の解をもつ．

点と直線の距離\(d\), 点\(P(x_{1},y_{1})\)と直線\(ax+by+c=0\)の距離\(d\)は

\(d=\displaystyle \frac{|ax_{1}+by_{1}+c|}{\sqrt{a^{2}+b^{2}}}\)

例

点\((1,4)\)を通り，\(3x+4y−5=0\)に平行・垂直な直線の方程式を求めよ．

傾きは\(-\displaystyle \frac{3}{4}\)となる．よって平行な直線は\(y-4=-\displaystyle \frac{3}{4}(x-1)\Leftrightarrow 3x+4y-19=0\)

垂直な直線は\(y-4=\displaystyle \frac{4}{3}(x-1)\Leftrightarrow 4x-3y+8=0\)

例

直線\(x−5y+8=0\)に関して点\(A(1,7)\)と対称な点\(B\)の座標を求めよ．

対称な点を\(B(a,b)\)とおく．

直線\(AB\)と\(x−5y+8=0\)は垂直に交わるので，\(\displaystyle \frac{7-b}{1-a}\cdot\frac{1}{5}=-1\)

また，\(AB\)の中点が\(x−5y+8=0\)に乗っているので，代入すると，\(\displaystyle \frac{a+1}{2}-5\cdot\frac{b+7}{2}+8=0\)

よって\(a=3,b=−3\)

例

点\((1,3)\)と直線\(5x−12y+5=0\)の距離\(d\)は

\(d=\displaystyle \frac{|5-12\cdot 3+5|}{\sqrt{5^{2}+12^{2}}}=\frac{|-26|}{13}=2\)

☆円と方程式

○円の方程式

点(a,b)を中心として，半径が\(r\)の円の方程式は\((x-a)^{2}+(y-b)^{2}=r^{2}\)となる．

またこれを展開すると，\(x^{2}+y^{2}-2ax-2by+a^{2}+b^{2}-r^{2}=0\)となる．一般的に\(x^{2}+y^{2}+lx+my+n=0\)の表す図形は円となる．

○円と直線

□交点

連立方程式を解けば，解は出てくる．

例

\(x^{2}+y^{2}=2\)と\(y=2x-1\)の交点は，\(x^{2}+(2x-1)^{2}=2\Leftrightarrow 5x^{2}-4x-1=0\Leftrightarrow(5x+1)(x-1)=0\)

\(x=-\displaystyle \frac{1}{5}\)のとき，\(y=-\displaystyle \frac{7}{5} x=1\)のとき，\(y=1\)

よって，\(\left(-\displaystyle \frac{1}{5},-\frac{7}{5}\right),~(1,1)\)

このように\(y\)もしくは\(x\)を消去して，二次方程式を作る．このとき判別式により交点の状態が分かる．

\(D>0\) ⇔ 異なる2点で交わる．\(D=0\) ⇔ 接する．\(D<0\) ⇔ 共有点をもたない．

例

\(x^{2}+y^{2}=2\)と\(y=2x+k\)が共有点をもつとき，\(k\)の範囲は

\(x^{2}+(2x+k)^{2}=2\Leftrightarrow 5x^{2}+4kx+k^{2}-2=0\)

\(D^{\prime}=(2k)^{2}-5(k^{2}-2)=-k^{2}+10\)

ここで共有点をもつ条件は\(D^{\prime}\geqq 0\)

よって\(-\sqrt{10}\leqq k\leqq\sqrt{10}\)

また交点の状態を調べるのに円の中心と直線の距離の関係で分かることがある．

半径rの円の中心と直線lの距離を\(d\)とすると，

\(d<r\) ⇔ 異なる２点で交わる．\(d=r\) ⇔ 接する．\(d>r\) ⇔ 共有点をもたない．

○円の接線

円 \((x-a)^{2}+(y-b)^{2}=r^{2}\)上の点\((x_{1},y_{1})\)におけるこの円の接線の方程式は

\((x_{1}-a)(x-a)+(y_{1}-b)(y-b)=r^{2}\)

例

点\((1,2)\)を通り，円 \(x^{2}+y^{2}=2\)に接する直線の方程式を求めよ．

まず接点をおこう．接点を\((a,b)\)とおくと，

\(a^{2}+b^{2}=2\)

また，この点における接線は\(ax+by=2\)となる．

この接線は点\((1,2)\)を通るので，代入する．

\(a+2b=2\)

よってこの\(a,b\)の連立方程式を解くと，

\((a,b)=\left(\displaystyle \frac{6}{5},\displaystyle \frac{2}{5}\right),~(2,0)\)

よって接線は\(\displaystyle \frac{6}{5}x+\frac{2}{5}y=2\Leftrightarrow 3x+y=5，x=1\)

○応用

2つの円 \(x^{2}+y^{2}=3\)…①　\(x^{2}+y^{2}-4x+6y+1=0\)…②の交点\(A,B\)と点\((2,1)\)を通る円の中心と半径を求めよ．

ここでは少し解き方が特殊ではあるが，まず\(k(x^{2}+y^{2}-3)+(x^{2}+y^{2}-4x+6y+1)=0\)とおく．

この式は①と②を代入すればわかるが，①かつ②を満たしている．つまり両方の交点を通るということになる．よってあとは点\((2,1)\)のついて考えればよい．

これも代入して計算すると，\(2k+4=0⇔k=−2\)

よって\(x^{2}+y^{2}+4x-6y-7=0\Leftrightarrow(x+2)^{2}+(y-3)^{2}=20\)

よって求める円の中心は\((−2,3)\)で半径は\(\sqrt{20}\)である．

☆軌跡と領域

○軌跡

点\(P\)の軌跡がある図形上に乗っていることを示すには

１，条件を満たす任意の点\(P\)は，図形上にある．

２，図形上の任意の点\(P\)は，その条件を満たしている．

あくまでも必要十分性を示す必要があるので，2のことを書かないといけない．

例

2点\(A(1,1),B(2,3)\)からの距離の比が\(3:2\)である点\(P\)の軌跡を求めよ．

まず，点\(P(x,y)\)とおく．

１，条件は\(AP:BP=3:2\)．つまり\(3BP=2AP\)

よって\(3\sqrt{(x-2)^{2}+(y-3)^{2}}=2\sqrt{(x-1)^{2}+(y-1)^{2}}\)

二乗して整理すると，\((x-4)^{2}+(y-7)^{2}=30\)．よって条件を満たす点はこの円上に存在する．

２，逆に計算をたどると，円上の任意の点は条件を満たしている．

以上より求める軌跡は\((x-4)^{2}+(y-7)^{2}=30\)である．

○領域

\(x,y\)の不等式で満たされている点\((x,y)\)全体の集合（条件を満たしている範囲）を領域という．

□直線・円と領域

直線\(y=mx+n\)において

１，不等式\(y>mx+n\)の表している領域は直線より上の部分

２，不等式\(y<mx+n\)の表している領域は直線より下の部分

円\((x-a)^{2}+(y-b)^{2}=r^{2}\)において

１，不等式\((x-a)^{2}+(y-b)^{2}<r^{2}\)の表している領域は円の内部

２，不等式\((x-a)^{2}+(y-b)^{2}>r^{2}\)の表している領域は円の外部

例

この不等式の表す領域を示せ．\((x-y+1)(x^{2}+y^{2}-4)<0\)

まず不等式について，\(x-y+1>0\) かつ \(x^{2}+y^{2}-4<0\) または \(x-y+1<0\) かつ \(x^{2}+y^{2}-4>0\)

\(x-y+1=0, x^{2}+y^{2}-4=0\)の両方の図形を描き，上の条件を満たしているところを斜線で引けばよい．

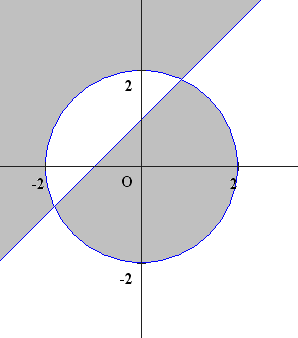等号はないので求める領域は灰色部分で境界線を含まない．

○領域と最大最少（この手の問題は難関大学でも出る．）

例

以下のような条件のもとで\(x+y\)の最大値，最小値を求めよ．

条件：\(x≧0,≧0,5x+2y≦7,2x+3y≦5\)

まず条件をグラフで表し，\(x+y=k\)として，\(k\)の範囲を求める．

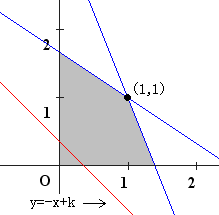この赤い線が\(x+y=k\)であるが，条件を満たしながら赤い線が動くには，灰色部分を一か所でも満たしていればいい．よって最小値は\((0,0)\)を通るときで，最大値は\((1,1)\)を通る時である．よって最小値は\(x=0,y=0\)のとき0で，最大値は\(x=1,y=1\)のとき2となる．

○領域を使った証明（論理集合を使う）

条件\(p\)を満たしている全体の集合を\(P\)とし，条件\(q\)を満たしている全体の集合を\(Q\)とすると，

｢\(p\)ならば\(q\)は真である｣ ⇔ \(P⊂Q\)（\(Q\)の範囲の中に\(P\)が含まれている）

例

\(x^{2}+y^{2}<1\)ならば\(y<1\)は真である．これはグラフを描けばわかるが，\(y<1\)のなかに\(x^{2}+y^{2}<1\)が含まれているからである．

もちろんこのような問題なら今回の方法を使うまでもないが，これを使わないと解けない問題もあるので，しっかりと覚えること．