MATH

コペルニクス　”太陽は宇宙の中心であって不動であり，太陽の運動と見えるものは全て実は地球の運動である．”

¶三角関数

☆角度・孤・面積

注　定義で覚えることが多いですが，これを覚えればあとはちょっと考えて変形させれば何とかなります．

○角度

いままでは度数法(180°など)を使っていましたが，これからは孤度法を使いましょう．

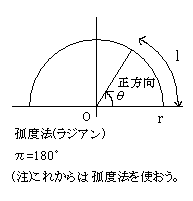
これは孤の長さをそのまま角度として使ったものです．上の図では半円を孤度法で言うと，この長さは\(\pi\)である．また\(180°\)でもあるので，\(\pi=180°\)となります．

○孤の長さ\(l=r\theta\)，面積\(S=\displaystyle \frac{1}{2}r^{2}\theta=\frac{1}{2}rl\) (証明は教科書に載っていると思うので知りたかったら教科書を開きましょう．)

☆三角関数の性質

ここら辺は全部丸暗記はきついので以下のように図で解決しよう．

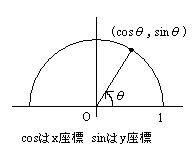
\(\cos\)は\(x\)座標,\(\sin\)は\(y\)座標と覚えよ．

円上だから\(−1≦\sin x≦1,−1≦\cos x≦1\)

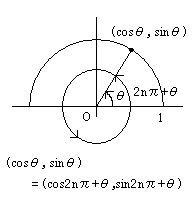(\(x,y\)座標ともに変わっていない．)

\(\sin(x+2n\pi)=\sin x \cos(x+2n\pi)=\cos x \tan(x+2n\pi)=\tan x\)（\(n\)は整数）

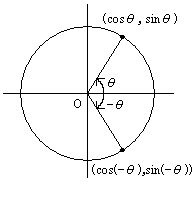(\(y\)座標が－に変化した．(\(\sin\)の符号が変化))

\(\sin(-x)=-\sin x \cos(-x)=\cos x \tan(-x)=-\tan x\)

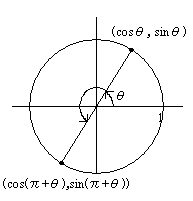(\(x,y\)座標ともに－に変化した．(\(\sin,\cos\)の符号が変化))

\(\sin(x+\pi)=-\sin x \cos(x+\pi)=-\cos x \tan(x+\pi)=\tan x\)

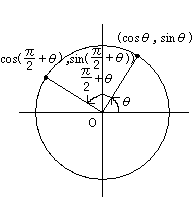(\(x\)座標が\(-y\)座標に変化，\(y\)座標が\(x\)座標に変化\((\cos\)が\(−\sin\)へ,\(\sin\)が\(\cos\)へ変化))

\(\sin(x+\displaystyle \frac{\pi}{2})=\cos x \cos(x+\frac{\pi}{2})=-\sin x \tan(x+\frac{\pi}{2})=-\frac{1}{\tan x}\)

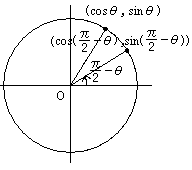
(\(x\)座標が－に変化した(\(\cos\)の符号が変化))

\(\sin(\pi-x)=\sin x \cos(\pi-x)=-\cos x \tan(\pi-x)=-\tan x\)

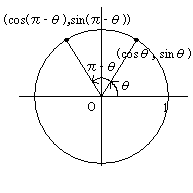
(\(x\)座標が\(y\)座標に変化，\(y\)座標が\(x\)座標に変化(\(\cos\)が\(\sin\)へ,\(\sin\)が\(\cos\)へ変化))

\(\sin(\displaystyle \frac{\pi}{2}-x)=\cos x \cos(\frac{\pi}{2}-x)=\sin x \tan(\frac{\pi}{2}-x)=\frac{1}{\tan x}\)

☆三角関数のグラフ

○補足

偶関数・奇関数(これは積分の時に有効活用できる．ここではあったな程度でOK)

偶関数とは\(y\)軸に対して対称

例　\(y=x^{2},y=\cos x\) (具体的にイメージしてみよう)

一般的に\(f(−x)=f(x)\)

奇関数とは原点に関して対称

例　\(y=x,y=\sin x,y=\tan x\) (具体的にイメージしてみよう)

一般的に\(f(−x)=−f(x)\)

○グラフ

\(y=\sin x\)

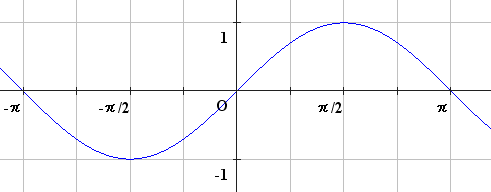
周期　\(2\pi\)

値域　\(−1≦y≦1\)

奇関数

\(y=\cos x\)

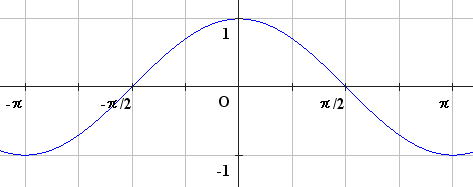
周期　\(2\pi\)

値域　\(−1≦y≦1\)

偶関数

\(y=\tan x\)

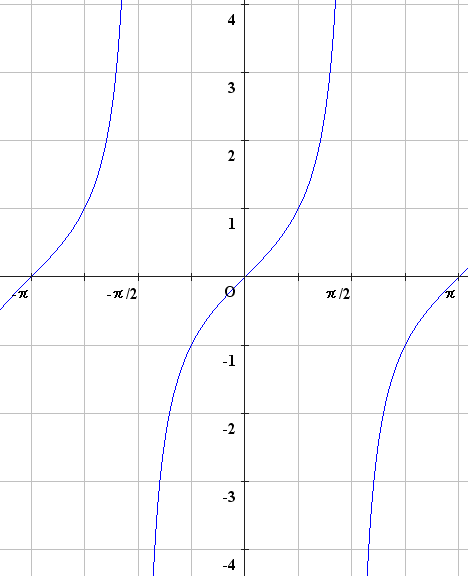
周期　\(\pi\)

漸近線　\(x=\displaystyle \frac{\pi}{2}+n\pi\)

奇関数

☆三角関数の公式

○三角関数の相互関係

\(\tan x=\displaystyle \frac{\sin x}{\cos x}\) (図から)

\(\sin^{2}x+\cos^{2}x=1\) (円から)

\(\displaystyle \rightarrow 1+\tan^{2}x=\frac{1}{\cos^{2}x}\) (両辺を\(\cos^{2}x\)で割った．)

○加法定理(証明は教科書に載っている．一応東大で証明問題として出されたが，個人的には覚えなくてもいいと思うのですが・・)

\(\sin(x+y)=\sin x\cos x+\cos x\sin y\)

\(\rightarrow \sin(x-y)=\sin x\cos y-\cos x\sin y\) (\(y\)を\(-y\)へ変えた．このとき，\(\sin(-x)=-\sin x \cos(-x)=\cos x\)を使った．)

\(\cos(x+y)=\cos x\cos y-\sin x\sin y\)

\(\rightarrow \cos(x-y)=\cos x\cos y+\sin x\sin y\) (\(y\)を\(-y\)へ変えた．)

\(\tan(x+y)=\displaystyle \frac{\tan x+\tan y}{1-\tan x\tan y}\) (\(\tan x=\displaystyle \frac{\sin x}{\cos x}\)を使う．)

\(\displaystyle \rightarrow \tan(x-y)=\frac{\tan x-\tan y}{1+\tan x\tan y}\) (\(y\)を\(-y\)へ変えた．)

○二倍角の定理

\(\sin 2x=2\sin x\cos x\) (加法定理で\(y=x\)にした．)

\(\cos 2x=\cos^{2}x-\sin^{2}x=1-2\sin^{2}x=2\cos^{2}x-1\) (加法定理で\(y=x\)にした．)

\(\tan 2x=\displaystyle \frac{2\tan x}{1-\tan^{2}x}\) (加法定理で\(y=x\)にした．)

○三倍角の定理

\(\sin 3x=3\sin x-4\sin^{3}x\) (加法定理をするとできる．)

\(\cos 3x=4\cos^{3}x-3\cos x\) (加法定理をするとできる．)

\(\tan 3x=\displaystyle \frac{3\tan x-\tan^{3}x}{1-3\tan^{2}x}\) (加法定理をするとできる．)

○半角の定理

\(\sin^{2}\displaystyle \frac{x}{2}=\frac{1-\cos x}{2}\) (二倍角の\(\cos 2x=1-2\sin^{2}x\)で\(x\displaystyle \rightarrow\frac{x}{2}\)とした．)

\(\cos^{2}\displaystyle \frac{x}{2}=\frac{1+\cos x}{2}\) (二倍角の\(\cos 2x=2\cos^{2}x-1\)で\(x\displaystyle \rightarrow\frac{x}{2}\)とした．)

\(\tan^{2}\displaystyle \frac{x}{2}=\frac{1-\cos x}{1+\cos x}\) (\(\tan x=\displaystyle \frac{\sin x}{\cos x}\)を使う．)

※これはよく\(t=\tan\displaystyle \frac{x}{2}\)とおいた問題が出る．

\(\sin x=\displaystyle \frac{2\tan\frac{x}{2}}{1+\tan^{2}\frac{x}{2}}\),\(\displaystyle \cos x=\frac{1-\tan^{2}\frac{x}{2}}{1+\tan^{2}\frac{x}{2}}\),\(\displaystyle \tan x=\frac{2\tan\frac{x}{2}}{1-\tan^{2}\frac{x}{2}}\)

☆直線の傾き

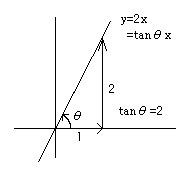図のように直線の傾き=\(\tan\)となる．これで2直線のなす角度などを求められる．

☆\(a\sin\theta+b\cos\theta\)の変形

ここは丸暗記でよい(と思う)．

\(a\sin\theta+b\cos\theta=\sqrt{a^{2}+b^{2}}\sin(\theta+\alpha)=\sqrt{a^{2}+b^{2}}\cos(\theta-\beta)\)

ただし\(\displaystyle \sin\alpha=\frac{b}{\sqrt{a^{2}+b^{2}}}\),\(\displaystyle \cos\alpha=\frac{a}{\sqrt{a^{2}+b^{2}}}\),\(\displaystyle \sin\beta=\frac{a}{\sqrt{a^{2}+b^{2}}}\),\(\displaystyle \cos\beta=\frac{b}{\sqrt{a^{2}+b^{2}}}\)である．

証明(見なくてよい．)

1，加法定理から

\(a\displaystyle \sin\theta+b\cos\theta=\sqrt{a^{2}+b^{2}}(\frac{a}{\sqrt{a^{2}+b^{2}}}\sin\theta+\frac{b}{\sqrt{a^{2}+b^{2}}}\cos\theta)=\sqrt{a^{2}+b^{2}}\sin(\theta+\alpha)\)

もう片方も同様にやればよい．

2，図から

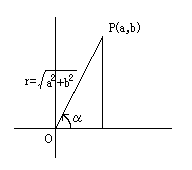\(OP=r\)とすると \(a=r\cos\alpha,b=r\sin\alpha\)　よって\(a\sin\theta+b\cos\theta=r\sin\theta\cos\alpha+r\cos\theta\sin\alpha=r(\sin\theta\cos\alpha+\cos\theta\sin\alpha)=\sqrt{a^{2}+b^{2}}\sin(\theta+\alpha)\)

(注：もう片方は\(a,b\)を入れ替えてかんがえればよい．)