MATH

ガウス　”他の人でも私のように深く，絶えず数学的真理に没頭すれば，同様になることができるはずです．”

¶複素数平面

〇基本的な複素数の性質
\(a,b\)を実数，\(i\)を虚数とすると，
一般的な虚数を\(\alpha=a+bi\)と置くことができる．
この時，共役な複素数は\(\bar{\alpha}=a-bi\)と置ける．
よって，\(\alpha\)が実数の時，\(\alpha=\bar{\alpha}\)
\(\alpha\)が純虚数の時，\(\alpha=-\bar{\alpha}\)，\(\alpha\neq 0\)


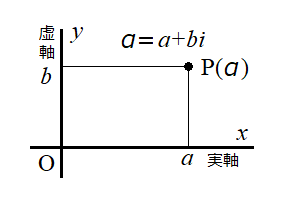
〇複素数平面
複素数\(\alpha=a+bi\)に対して，\(x\)軸を実軸，\(y\)軸を虚軸とする時，座標平面上に点\((a,b)\)を対応させる．点の表記方法として，\(P(\alpha)\)，\(P(a+bi)\)と書く．

〇複素数の和，差
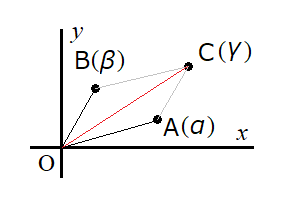
複素数平面上の点を\(A(\alpha)\)，\(B(\beta)\)，\(C(\gamma)\)，\(D(\delta)\)とする．
和：\(\gamma=\alpha+\beta\)の場合，図に示す点となる．

差：\(\delta=\alpha-\beta\)の場合，図に示す点となる．

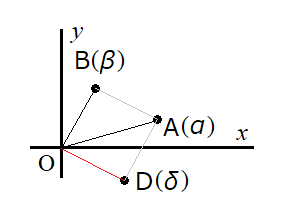
(ベクトルと同じイメージでよい)

〇複素数の実数倍
・実数倍
複素数\(\alpha=a+bi\)に対して，\(k\alpha=ka+kbi\)（\(\alpha \neq 0,~k\)は実数）

・共線
3点\(0,\alpha,\beta\)が一直線上にある場合，\(\beta=k\alpha\)が成立する．（\(\alpha \neq 0,~k\)は実数）

〇複素数の絶対値と距離
・絶対値
複素数\(\alpha\)に対して，絶対値\(|\alpha|\)は複素数平面の原点からの距離となる．つまり，次のようになる．
\(|\alpha|\)\(=|a+bi|\)\(=\sqrt{a^2+b^2}\)
また，次のような性質を持つ．
\(|\alpha|\)\(=|-\alpha|\)\(=|\bar{\alpha}|\)
\(\alpha\bar{\alpha}\)\(=|\alpha|^2\)
・2点間の距離
複素数\(\alpha,\beta\)に対して，複素数平面上の距離は\(|\beta-\alpha|\)となる．

○極形式
\(z=a+bi\)に対して，原点\(O\)，点\(P(a,b)\)，\(OP=r\)とすると，
極形式：\(a+bi\)\(=r(\cos\theta +i\sin\theta\))
絶対値：\(r=|z|=\sqrt{a^2+b^2}\)
偏角：\(\theta=\arg z\)
（\(\displaystyle \cos \theta=\frac{a}{\sqrt{a^2+b^2}}\)，\(\displaystyle \sin \theta=\frac{b}{\sqrt{a^2+b^2}}\)）

\(\theta \rightarrow -\theta\)とすると，
\(\bar{z}=r(\cos(-\theta)+i\sin(-\theta))\)\(=r(\cos\theta-i\sin\theta)\)
\(\arg \bar{z}=-\arg z\)

〇複素数の積，商
\(z_1=r_1(\cos\theta_1 +i\sin\theta_1)\)，\(z_2=r_2(\cos\theta_2 +i\sin\theta_2)\)と置くとき，

積：\(z_1z_2=r_1r_2(\cos(\theta_1+\theta_2) +i\sin(\theta_1+\theta_2)\)
絶対値：\(|z_1z_2|=|z_1||z_2|\)
偏角：\(\arg(z_1z_2)=\arg z_1 +\arg z_2\)


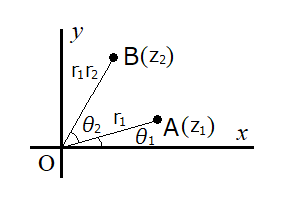
商：\(\displaystyle \frac{z_1}{z_2}=\frac{r_1}{r_2}(\cos(\theta_1-\theta_2) +i\sin(\theta_1-\theta_2))\)
絶対値：\(\displaystyle \left|\frac{z_1}{z_2}\right|=\frac{|z_1|}{|z_2|}\)
偏角：\(\displaystyle \arg\left(\frac{z_1}{z_2}\right)=\arg z_1 -\arg z_2\)



★図形的意味
複素数の和と差⇒平行移動
複素数の積と商⇒回転と拡大・縮小

〇ド・モアブルの定理
\(n\)を整数とする時，次の式が成立する．
\((\cos \theta +i \sin\theta)^n=\cos n\theta +i \sin n\theta\)
※単純に\(k=1,2,\cdots,n\)において，\(r_k=1\),\(\theta_k=\theta\)で複素数の積を\(n\)回繰り返す．
★\(z^n=1\)の解について
\(z^n=1\)の解は，複素平面上に単位円を描くと，初期点\((1,0)\)から角度で\(n\)分割された各点が解となる．
よって，角度が小さい順で\(k\)番目の解\(z_k\)は\(\displaystyle z_k=\cos\left(\frac{2\pi k}{n}\right)+i\sin\left(\frac{2\pi k}{n}\right)\)となる．（\(k=1,2,\cdots, n-1\)）
★応用:\(z^n=r(\cos\theta+i\sin\theta)\)の解について
複素平面上に半径\(^{n}\sqrt{r}\)の円を描くと，初期点の角度\(\displaystyle \frac{\theta}{n}\)から角度で\(n\)分割された各点が解となる．
よって，角度が小さい順で\(k\)番目の解\(w_k\)は\(\displaystyle w_k=^{n}\sqrt{r}\cos\left(\frac{\theta}{n}+\frac{2\pi k}{n}\right)+i\sin\left(\frac{\theta}{n}+\frac{2\pi k}{n}\right)\)となる．（\(k=1,2,\cdots, n-1\)）

また，\(w_k=w_0z_k\)が成立する．


〇複素数と図形
複素数平面上の点を\(A(\alpha)\)，\(B(\beta)\)，\(C(\gamma)\)，\(D(\delta)\)とする（互いに異なるとする）．
・線分の分点
基本的に通常の線分と同じ．
内分点：\(m:n\)の比に内分する点\(P(z)\)は\(\displaystyle z=\frac{n\alpha+m\beta}{m+n}\)
外分点：\(m:n\)の比に外分する点\(Q(z)\)は\(\displaystyle z=\frac{-n\alpha+m\beta}{m-n}\)
\(△ABC\)の重心\(G(g)\)：\(\displaystyle w=\frac{\alpha+\beta+\gamma}{3}\)

・2直線の関係
偏角：\(\displaystyle \angle BAC=\arg\left(\frac{\gamma-\alpha}{\beta-\alpha}\right)\)
共線：\(A,B,C\)が一直線上にある場合，\(\displaystyle \frac{\gamma-\alpha}{\beta-\alpha}\)が実数（偏角が\(0,\pi\)）
平行：\(AB//CD\)\(\Leftrightarrow\) \(\displaystyle \frac{\delta-\gamma}{\beta-\alpha}\)が実数（偏角が\(0,\pi\)）
垂直：\(AB\perp AC\)\(\Leftrightarrow\) \(\displaystyle \frac{\gamma-\alpha}{\beta-\alpha}\)が純虚数（偏角が\(\displaystyle \pm\frac{\pi}{2}\)）

・等式の表す図形
\(|z-\alpha|=r\)は点\(\alpha\)を中心として，半径\(r\)の円．
\(|z-\alpha|=|z-\beta|\)は2点\(\alpha,\beta\)を結ぶ線分の垂直二等分線