MATH

カントール　”数学の本質は，その自由性にある．”

¶集合と論理

☆集合…何か（要素）の集まり

例　偶数　成績80～90点の人

集合\(A\)は2～10以内の偶数であるは

\(A=\{2,4,6,8,10\}\)もしくは\(\{2n|1≦n≦5,nは自然数\}\)と表せる．

さらに集合\(B\)は8の正の約数であるは

\(B=\{1,2,4,8\}\)となる．

ここで，\(2,4,6,8,10∈A\)　\(1,2,4,8∈B\)（これを属するという）

¶場合の数

ここではやり方というより問題をたくさんやりパターンを覚えなければならないことが多いので，よく覚えること．1つの問題にもいろいろなアプローチに仕方があります．

☆場合の数

○樹形図

赤いボール1つと白いボール2つを並べる方法

赤白白　白赤白　白白赤　の3通りがあるが，これを次のようにあらわすと楽である．

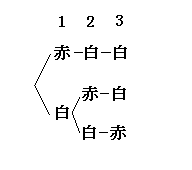
①1番目は赤か白．②2番目（１）赤の次は必ず白白（２）白の次は赤白か白赤

これで3通りであると整理できる．ここでは数が少ないのでありがたみはわからないが，たくさんある場合はこのように整理すれば漏れはなくなる．

センター試験では使える方法である．

○和の法則・積の法則

和の法則は同時におこらないことに関して場合の数を足すことで，積の法則は同時におこることに関して場合の数を掛けることである．

サイコロを二回振る時の目の和が5の倍数のときは

和が①5の時②10の時の2つがある．①のときは1+4，2+3，3+2，4+1の4通り②のときは4+6，5+5，6+4の3通り

ここでこの①，②は同時におこらない．（和が同時に5と10でてたら変でしょ．）よって4+3=7通り（和の法則）

コインを２回振る時に全部で何通り出るか．

①1回目は表裏で2通り②2回目は表裏で2通り

ここでこの①，②は同時におこる．（1回目おきてから，2回目がおこる）よって2×2=4通り（積の法則）

○順列

\(n\)個から\(r\)個とりだして並べるとき\({}_{n}P_{r}=n(n-1)\cdots(n-r)\)とかく．特に\({}_{n}P_{n}=n!\)とかく．

また\({}_{n}P_{r}=\displaystyle \frac{n!}{(n-r)!}\)とも書ける．他に\(0!=1，{}_{n}P_{0}=1\)とする．

1～5の数字から3つ取って3桁の数字を作る時，5個から3個とりだして並べるので，\({}_{5}P_{3}=5\times 4\times 3=60\)通りとなる．

○円順列（数珠順列）

例　4人が輪を作る時の並び方

考え１　まず普通に順列を考えると\({}_{4}P_{4}=24\)通りだが，輪の時は同じ並びが４つできる（図を描けばわかる）．

よって\(\displaystyle \frac{{}_{4}P_{4}}{4}=6\)通りとなる．

考え２　１人を固定すると同じ並びはできない．（回転して同じ並びはできない．）

よって\({}_{3}P_{3}=6\)通り

以上から円順列は一般的に\(\displaystyle \frac{{}_{n}P_{n}}{n}=(n-1)!\)となる．

もし人でなく赤青黄白のように区別のつく４つの球を数珠のようにつなげると表裏も考えるので，6÷2=3通り（ただし一般に2で割るのではないので注意．）

○重複順列

\(n\)個から\(r\)個繰り返し同じものを許して取り出せて並べるとき\(n^{r}\)通りとなる．

1～5の数字から繰り返し同じものをとってもよいとして（重複を許す）3つ取って3桁の数字を作る時，\(5^{3}=125\)通りとなる．

○組合せ

\(n\)個から\(r\)個順番を考えずとりだすとき（選び出す）\({}_{n}C_{r}=\displaystyle \frac{{}_{n}P_{r}}{r!}=\frac{n(n-1)\cdots(n-r+1)}{r(r-1)\cdots 2\cdot 1}\)とかく．特に\({}_{n}C_{n}=1\)

また\({}_{n}C_{r}=\displaystyle \frac{n!}{r!(n-r)!}\)とも書ける．他に性質として\({}_{n}C_{r}=_{n}C_{n-r}\)（0≦ｒ≦n）\({}_{\text{，　}n}C_{r}={}_{n-1}C_{r-1}+{}_{n-1}C_{r}\) \((1≦r≦n−1,n≧2)\)となる．

赤いボール6つから4つを取り出すとき，順番は考えないから\({}_{6}C_{4}={}_{6}C_{2}=\displaystyle \frac{6\times 5}{2\times 1}=15\)通りとなる．

例　5つの色の違うボールペンを

(1)\(A\)の箱に2つ，\(B\)の箱に2つ，\(C\)の箱に1つ入れて分ける．

(2)2つ2つ1つに分ける．

(1)まず5個のうちに２つ選び出し\(A\)にいれ，3つから2つ選びだし\(B\)にいれ，1つは残りの箱に入れればいい．これは積の法則から

\({}_{5}C_{2}\times {}_{3}C_{2}\times 1=30\)通り

(2)(1)の問題に対して，A,B,Cのように区別がない．ここで同じものが2通りあるので，(2・2・1を並べる時２は同じなのでかぶる．よって2!で割る)

30÷2=15通り

例　赤いボール1つ，白いボール2つ，黒いボール2つを並べる方法

これは5つの場所にどのようにボールをおくかを考える．5つの場所のうちに黒いボールを2つ．次に3つの場所に白いボールを2つ余ったところに1つ入れればよい．

よって，\({}_{5}C_{2}\times {}_{3}C_{2}\times {}_{1}C_{1}=30\)通り

また違う考え方もできる．5つをまず並べるが，その時に黒いボールと白いボールは見分けがつかないので，余分な分を割らなくてはならない．このとき，それぞれ２つなので，黒いボールが「異なる」と考えたときの\(2!\)分余分に数えていることになる．よって\(\displaystyle \frac{5!}{2!\times 2!\times 1!}=30\)通り

○重複を許して取る組み合わせ

これは異なる\(n\)個から異なる\(r\)個を取り出したとき同じものを繰り返しとっても良いという条件のもとで考える問題である．

たとえば，\(a,b,c\)の数字から６個とる組み合わせの総数を考えるとする．このとき考え方として，１が何個，２が何個，…という数え方をしないで，ボールと仕切りを考えることにする．図を描けばこのようになる．\(a\)のゾーン|\(b\)のゾーン|\(c\)のゾーン（例: \(a\)が２つ，\(b\)が３つ，\(c\)が１つのとき→○○|○○○|○，\(b\)が２つ，\(c\)が４つのとき→|○○|○○○○）このように考えると６つのボールと２つの仕切りをならべる方法に等しい．よって\({}_{8}C_{2}={}_{8}C_{6}=28\)通りとなる．

一般的に異なる\(n\)個から異なる\(r\)個を取り出したとき同じものを繰り返しとっても良い場合の総数は\({}_{n+r-1}C_{r}\)とおりである．

※違う考え方（１が何個，２が何個，…という数え方）

１が\(k\)個あるとする．すると，残り\(6−k\)個で2と3を選べばよい．この時は選び方は\(7−k\)通りある．またkは0～6まで可能である．よって総数は\(\displaystyle \sum_{k=0}^{6}(7-k)=28\)通り．

このやり方は難関大学でもよく出る．

○二項定理

\((a+b)^{3}=a^{3}+3a^{2}b+3ab^{2}+b^{3}\)という公式は分かっていると思うが，この求め方を別の考え方で考えると３乗以外もわかるようになる．

\((a+b)^{3}=(a+b)(a+b)(a+b)\)とする．例えば，\(a^{2}b\)の係数が知りたいというとき，\(a^{2}b\)は\(a\)を２つ，\(b\)を１つ取り出すことに等しい．つまりこれは\({}_{3}C_{2}={}_{3}C_{1}\)個ある．よって係数は\({}_{3}C_{2}={}_{3}C_{1}=3\)となる．これを一般的にしたのが二項定理である．つまり

\((a+b)^{n}={}_{n}C_{0}a^{n}+{}_{n}C_{1}a^{n-1}b+\displaystyle \cdots+{}_{n}C_{n-1}ab^{n-1}+{}_{n}C_{n}b^{n}=\sum_{k=0}^{n}{}_{n}C_{k}a^{n}{}^{-k}b^{k}\)となる．

二項定理の応用として\(2^{n}=(1+1)^{n}={}_{n}C_{0}+{}_{n}C_{1}+\cdots+{}_{n}C_{n}，0=(1-1)^{n}={}_{n}C_{0}-{}_{n}C_{1}+\cdots+(-1)^{n}{}_{n}C_{n}\)などがある．

また上と同じように考えると\((a+b+c)^{n}\)も求められる．\(a^{s}b^{t}c^{u}\)の係数は\(\displaystyle \frac{(s+t+u)!}{s!t!u!}\)となる． ただし\(s+t+u=n\)