MATH

ゲーテル　”Either mathematics is too big for the human mind, or the human mind is more than a machine”

¶論理と集合

☆集合…ものの集まりのこと．

集合は図を書くとわかりやすいので，書いた方がよい．

その集合を形成している1つ1つのものを要素という．

また，集合\(A\)に\(a\)が属していて，\(b\)が属していない時

\(A\in a,A\not\in b\)と書く．

例

1年4組の益男くん(\(a\))と5組の英臣くん(\(b\))について

1年という集合\(A\)には二人とも含まれているが，

4組という集合\(B\)には英臣君は含まれていない．

\(A\in a,A\in b,~B\in a,B\not\in b\)

○部分集合

\(x\in A\Rightarrow x\in B\)のときは\(A\)の中のすべての要素が\(B\)に入っている．

このとき，\(A\)は\(B\)の部分要素といい，\(A⊂B\)と書く．

また，\(A\)と\(B\)の要素が一致しているとき\(A=B\)と書く．

例

1年4組という集合\(B\)は1年という集合\(A\)に含まれている．

言い換えると，1年の要素は4組の要素を含んでいると言える．よって\(A⊂B\)となる．

○共通部分・和集合

ある集合が\(A\)と\(B\)両方に属しているとき\(A∩B\)と書く．(共通部分)

ある集合が\(A\)と\(B\)いずれか(少なくとも一方)に属しているとき\(A∪B\)と書く．(和集合)

もちろん2つ以上の場合もある．集合は図をかくとわかりやすい．(ベン図)

また要素が全くない場合は空集合\(\phi\)とかく．

例

1年の集合を\(A\)，4組の集合を\(B\)，学級委員の集合を\(C\)とすると，隆太郎くんは1年4組学級委員なので，\(A∩B∩C\)に含まれている．

卓くんは1年であるけど，5組でほかの委員会である．これは\(A∪B∪C\)に含まれているともいう．

○補集合

全体集合を\(U\)と決めた時，その中に含まれている集合\(A\)に対してこの\(A\)に属していない集合を\(\overline{A}\)(補集合)と書く．

例

1年全体の集合を\(U\)と決めた時，4組の集合を\(A\)とする．

1年が1～4組まであるとき，1～3組の集合は\(\overline{A}\)と表せる．

○ド・モルガンの法則

図を描けばわかるが次のような式が成り立つ．

\(\overline{A\cup B}=\overline{A}\cap\overline{B},\overline{A\cap B}=\overline{A}\cup\overline{B}\)

○集合の個数

集合\(A\)の個数を表すとき\(n(A)\)と書く．

なお個数について以下のような式が成り立つ．

\(n(A∪B)=n(A)+n(B)−n(A∩B)\)

※なお，\(A∩B=\phi\)のとき，\(n(A∪B)=n(A)+n(B)\)となる．

\(n(\overline{A})=n(U)−n(A)\)

☆論理

ここではセンターに出るのでしっかり学んでほしい．しかし，センターレベルまでしか出ないと考えてよいので，ここをクリアーすれば心配することはないはず．

○命題…ある文章に対して正しい(真)か正しくないか(偽)が決まるもの

命題の真偽を確かめるとき，

真の場合…証明する．

偽の場合…証明か成り立たないもの(反例)を1つあげる．

\(p,q\)の条件のもと，\(p,q\)を満たす集合をそれぞれ\(P,Q\)とするとき

(\(p⇒q\)が真) ⇔ (\(P⊂Q\)) ⇔ (\(q\)は\(p\)であるための必要条件，\(p\)は\(q\)であるための　十分条件)

(\(q⇒p\)が真) ⇔ \((Q⊂P)\) ⇔ (\(p\)は\(q\)であるための必要条件，\(q\)は\(p\)であるための　必要条件)

(\(p⇔q\)が真) ⇔ \((P=Q)\) ⇔ (\(q\)は\(p\)であるための必要十分条件，\(p\)は\(q\)であるための　必要十分条件)

※必要十分条件は言葉で見るとわかりにくいですが，以下のように見るといいでしょう．

なおこれが必ずわかるやり方かといわれるとアレですが，私はこの考え方でやってました．

\(p\)は\(q\)であるための○○条件である．と書いてあるとき，

\(p⇒q\)が成り立つとき，十分条件

\(q⇒p\)が成り立つとき，必要条件

となる．

例

\(x^{2}=4\)は\(x=2\)であるための○○条件と書いてあるとき，\(x=2⇒x^{2}=4\)が成り立つので，必要条件である．

○逆・裏・対偶

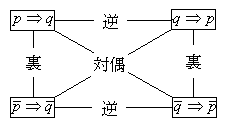
命題\(p⇒q\)において

\(q⇒p\)を逆

\(\overline{p}\Rightarrow\overline{q}\)を裏

\(\overline{q}\Rightarrow\overline{p}\)を対偶という．

なお命題\(p⇒q\)の証明をするとき，対偶\(\overline{q}\Rightarrow\overline{p}\)を証明してもよい．(図を書くとわかる．)

例

\(x−y≠3⇒x≠5\)または\(y≠2\)を証明するとき，

対偶は\(x=5\)かつ\(y=2⇒x−y=3\)となる．これは真なので，命題は真．

○背理法

ある事柄を証明するときその事柄が成り立たないことを仮定し，矛盾を導くことによりその事柄が成り立つことを示す証明法．

例題

\(\sqrt{2}\)が無理数であることを証明せよ．

答え

まず，\(n\)が整数であるとき，\(n^{2}\)が偶数⇒\(n\)も偶数であることを証明する．(対偶からの証明)

対偶をとると，\(n\)が奇数⇒\(n^{2}\)が奇数　これを証明する．

\(n=2k+1\)とすると，\(n^{2}=(2k+1)^{2}=2(2k^{2}+2k)+1\)

よって\(n^{2}\)は奇数となるので，\(n^{2}\)が偶数⇒\(n\)も偶数は成り立つ．

次に\(\sqrt{2}\)が有理数であると仮定すると，\(\displaystyle \sqrt{2}=\frac{m}{n}\)（\(m,n\)は互いに素な自然数）とおける．(背理法)

二乗して，変形すると\(2n^{2}=m^{2}\)．\(m,n\)は互いに素なので，\(m=2m^{\prime}\)とおける．\(∴n^{2}=2m^{\prime 2}\)

\(m,n\)は互いに素なので，\(m^{\prime},n\)も互いに素．よって\(n=2n'\)とおける．

しかし\(m\)と\(n\)が2の倍数となり互いに素であることに矛盾する．よって，\(\sqrt{2}\)は無理数である．

※

背理法より，\(a,b,c,d\)が有理数，\(\sqrt{m}\)は無理数であるとすると，

\( a+b \sqrt{m}=c+d \sqrt{m} \Rightarrow a=c,b=d \)が成り立つ．