MATH

ピタゴラス　”万物は流転する”

¶平面図形

☆平面図形

ここの内容はセンターレベルまでできればよい．なおセンターで使用する公式はかなり限られているので，その中からしっかりと解く力を身につけよう！

それぞれの証明方法を知りたければ教科書などを見よう．証明はあまり重要ではないけど．

それと問題の答えがない場合がありますが，これは結構有名なものなので，調べられると思い載せませんでした．実際そういうのは解かなくても大丈夫だと思います．

あと，平面図形がどのくらいまで解ければいいかというと教科書レベルで十分です．なおセンターでは三角比や三平方の定理などを混ぜる場合が多いのでセンターの過去問をやった方が実践的です．センターに出るようなものは(センター)と記しますが，出る・出ないの保証はできません．

○内分・外分

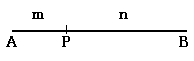
直線\AB\)を基準とする．

□内分

\(AP:PB=m:n\)

□外分

\(AP:PB=m:n\)

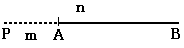
\(↑m>n\)のとき

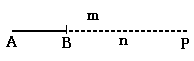
\(↑m<n\)のとき

☆三角形

○角の二等分線(センター)

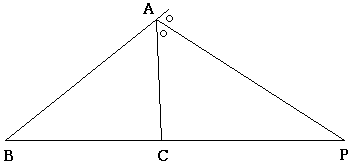
\(△ABC\)の\(∠A\)の二等分線と\(BC\)の交点を\(P\)とすると，\(AB:AC=BP:PC\)となる．

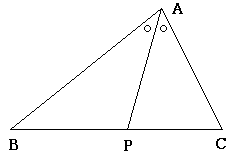
○三角形の五心(性質を覚えておこう．上から3つが重要)

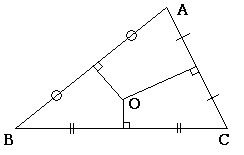
□外心(センター)

三角形の全ての辺の垂直二等分線の交点\(O\)のこと．

\(O\)は半径\(AO=BO=CO\)の円の中心．

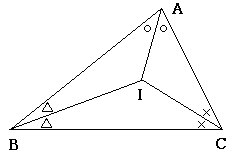
□内心(センター)

三角形のそれぞれの内角の二等分線の交点\(I\)のこと．

\(I\)は三角形\(ABC\)に内接する円の中心．

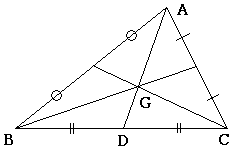
□重心(センター)

三角形のそれぞれの中線の交点\(G\)のこと．

性質としては中線について\(AG:GD=2:1\)．他の中線も同様．

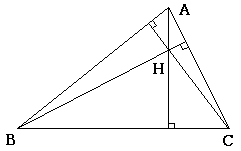
□垂心

各頂点から垂線を下ろしたときできる交点\(H\)のこと．

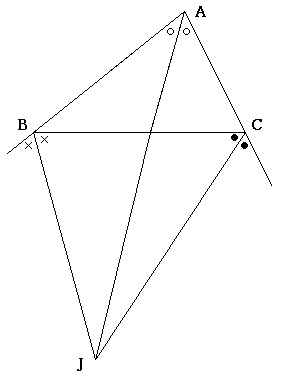
□傍心

１つの内角二等分線と，2つの外角二等分線の交点\(J\)のこと．

なお傍心は3つある．

問題

１，正三角形の外心・内心・重心・垂心は一致することを示せ．

２，三角形の外心\(O\)，重心\(G\)，垂心\(H\)は一直線上にあり，\(OG:GH=1:2\)であることを示せ．(この直線をオイラー線という)

３，傍心にある図において内心を\(I\)とすると，\(∠IBJは90°\)になることを示せ．

○三角形の辺と角の大小関係

一般的に三角形\(ABC\)において頂点の対角上にある辺を各文字の小文字であらわすことが多い．

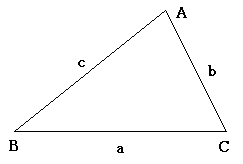
\(∠B＜∠C⇔b<c\)などの関係が成り立つ．

また，\(|a−b|<c<a+b\)などの関係が成り立つ．(この関係を三角不等式という．図形でなく，不等式の証明で意外と重要．)

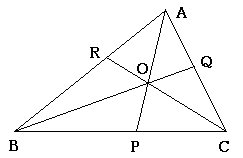
○メネラウスの定理

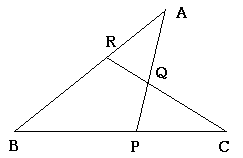
下のような図において以下のような等式が成り立つ．

\(\displaystyle \frac{BC}{CP}\cdot\frac{PQ}{QA}\cdot\frac{AR}{RB}=1\)　なお，証明方法は\(RQ\)に平行な直線を頂点\(C\)から引いて，\(AB\)との交点を決める．それから線分の比の関係から求められる．

○チェバの定理

このように各頂点から対角の辺に線を引いたときに図のように一点\(O\)に交わる．(五心とは一般的に関係ない．)

このとき，\(\displaystyle \frac{BP}{PC}\cdot\frac{CQ}{QA}\cdot\frac{AR}{RB}=1\)がなりたつ．証明方法は面積から求める方法やメネラウスの定理から求まる．(多分…)

☆円

円の孤と円周角などに関することは中学でやっている(はずな)ので，ここでは省略する．知りたいなら教科書を見ること．

○円に内接する四角形(センター)

図の●の角は等しい．また，対角の和は180°である．

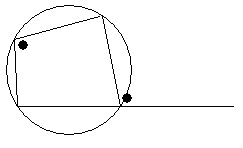
また，この逆も成り立つ．つまり，図の●の角は等しい．また，対角の和は180°であるならば，四角形が円に内接する．

※逆について

逆とは論理のところにありますが，条件\(p,q\)において\(p⇒q\)の逆であるから，\(q⇒p\)となる．

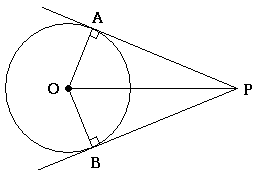
○円の接線(センター)

円の接線は接点と円の中心の線と垂直となる．この逆も成り立つ．

なお下の図で接線の長さ\(PA,PB\)は\(PA=PB\)の関係が成り立つ．

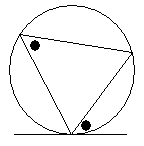
○接線と弦の作る角(センター)

図の角度●は等しい．

○方べきの定理(センター)

方べきの定理は以下の式が成り立つ．また，逆も成り立つ．

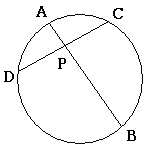
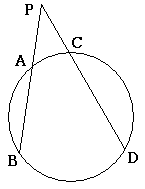
この図において\(PA\cdot PB=PC\cdot PD\)が成り立つ．

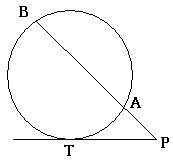
この図において\(PA\cdot PB=PT^{2}\)が成り立つ．

○円と直線・円と円の関係

ここは図形と方程式で問題としてよく扱われるので，詳しくは省略する．

なお，図形と方程式において

円と直線の接点・円と円が接する(内接・外接)条件では解が2つ出てくる場合があるので注意．

また，円2つと接する直線を共通接線というが，これは4本まで存在するので厄介である．