中級者
数学Ⅲ:様々な曲線
-
ヒント:これは\(t\)の関数と考えて,実数解\(t\)を持つときの\(x,y\)の動く範囲を考える.
問題
実数\(t\)に関して\(tx+(1-t^{2})y=1+t^{2}\)を満たすときの\((x,y)\)の動く範囲を求めよ.
解答
変形すると,\((1+y)t^{2}-xt+1-y=0\)
ここで,\(t\)が実数解を持つときの\(x,y\)の動く条件を考える.
これは判別式\(D \geqq 0\)が条件なので,
\(D=x^{2}-4(1+y)(1-y)=x^{2}+4y^{2}-4\geqq 0\)
よって動く範囲は\(\displaystyle \frac{x^{2}}{4}+y^{2}\geqq 1\)である.
参考入試問題
\(0 \leqq t \leqq 1\)を満たす実数\(t\)に対して,\(xy\)平面上の点\(A,B\)を
\(A\left(\displaystyle \frac{2(t^{2}+t+1)}{3(t+1)},-2\right)\),\(\displaystyle B\left(\frac{2}{3}t,-2t\right)\)
と定める.\(t\)が\(0 \leqq t \leqq 1\)を動くとき,直線\(AB\)の通りうる範囲を図示せよ.(1997 東大)
直線\(AB\):\(y=3(t+1)(t-1)x-2t^{3}\)
これを\(t\)について変形すると,\(2t^{3}-3t^{2}x+3x+y=0\)
これは\(0 \leqq t \leqq 1\)の間で\(2t^{3}-3t^{2}x+3x+y=0\)が実数解を持つときの範囲であると言いかえられる.
\(f(t)=2t^{3}-3t^{2}x+3x+y\)とおくと,\(f'(t)=6t(t-x)\)
1.\(0<x<1\)のとき
\begin{array}{c|c|c|c|c|c}
t & 0 & \cdots & x & \cdots & 1 \\ \hline
y'& 0 & - & 0 & + & 0 \\ \hline
y &3x+y & \searrow& -x^{3}+3x+y &\nearrow& y+2 \\ \hline
\end{array}
よって条件は\(-x^{3}+3x+y\leqq 0\)かつ(\(3x+y\geqq 0\)また\(y+2\geqq 0\))
2.\(x \geqq 1\)のとき
\begin{array}{c|c|c|c|c|c}
t & 0 & \cdots & 1 \\ \hline
y'& 0 & - & 0 \\ \hline
y &3x+y & \searrow& y+2 \\ \hline
\end{array}
よって条件は\(3x+y\geqq 0\)かつ\(y+2\leqq 0\)
3.\(x \leqq 0\)のとき
\begin{array}{c|c|c|c|c|c}
t & 0 & \cdots & 1 \\ \hline
y'& 0 & + & 0 \\ \hline
y &3x+y & \nearrow& y+2 \\ \hline
\end{array}
よって条件は\(3x+y\leqq 0\)かつ\(y+2\geqq 0\)
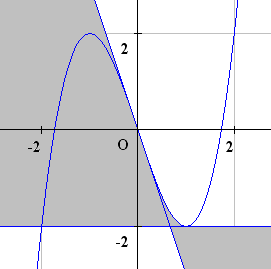
以上を図示すると次のようになる.