中級者
数学Ⅲ:微分法
-
ヒント:折り曲げる前も図に描くこと.折り曲げ前後で同じ角度になることを利用しよう.
問題
中心を\(O\)とした線分\(AB\)を直径とする半円がある.点\(A\)と周上の点\(C\)を結ぶ直線で折り曲げるときに,折り曲げた部分と半円とが重なる面積が最大となるとき,\(\cos \angle OAC\)を求めよ.(オリジナル)
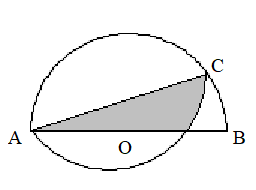
解答
\(\angle OAC=x\)とする.
(1) \(\displaystyle 0\leqq x<\frac{\pi}{4}\)の時,
折り曲げた部分を戻した図は次のようになる.
よって,図の灰色部分の面積を求めればよい.

半径を\(r\),面積を\(S(x)\)と置くと,
三角形OACの面積\(=\displaystyle \frac{1}{2}r^2\sin \angle AOC\)\(=\displaystyle \frac{1}{2}r^2\sin(\pi-2x)\)\(=\displaystyle \frac{1}{2}r^2\sin 2x\)
扇形OBCの面積\(=\displaystyle \frac{1}{2}r^2\angle BOC\)\(=\displaystyle \frac{1}{2}r^2 2x\)
三角形OADの面積\(=\displaystyle \frac{1}{2}r^2\sin \angle AOD\)\(=\displaystyle \frac{1}{2}r^2\sin(\pi-4x)\)\(=\displaystyle \frac{1}{2}r^2\sin 4x\)
扇形OBDの面積\(=\displaystyle \frac{1}{2}r^2\angle BOD\)\(=\displaystyle \frac{1}{2}r^2 4x\)
よって,\(S(x)\)=三角形OADの面積+扇形OBDの面積-(三角形OACの面積+扇形OBCの面積)\(=\displaystyle \frac{1}{2}r^2(\sin 4x-\sin 2x+2x)\)
\(S'(x)\)\(=\displaystyle r^2(2\cos 4x-\cos 2x+1)\)\(=\displaystyle r^2(4\cos^2 2x-\cos 2x-1)\)
ここで,\(S'(a)=0\)となる\(\cos 2a\)は,\(\displaystyle 0\leqq x<\frac{\pi}{4}\)より,\(\displaystyle \cos 2a=\frac{1+ \sqrt{17}}{8}\)
一方で,\(0\leqq x<a\)の時,\(S'(x)>0\),\(\displaystyle a\leqq x<\frac{\pi}{4}\)の時,\(S'(x)<0\)なので,\(x=a\)で極大値となる.
(2) \(\displaystyle \frac{\pi}{4}\leqq x \leqq \frac{\pi}{2}\)の時,
折り曲げた部分を戻した図は次のようになる.
よって,図の灰色部分の面積を求めればよい.

三角形OACの面積\(=\displaystyle \frac{1}{2}r^2\sin \angle AOC\)\(=\displaystyle \frac{1}{2}r^2\sin(\pi-2x)\)\(=\displaystyle \frac{1}{2}r^2\sin 2x\)
扇形OACの面積\(=\displaystyle \frac{1}{2}r^2\angle AOC\)\(=\displaystyle \frac{1}{2}r^2(\pi-2x)\)
よって,\(S(x)\)=扇形OACの面積-三角形OACの面積\(=\displaystyle \frac{1}{2}r^2(\pi-2x)-\sin 2x\)
\(S'(x)\))\(=\displaystyle -r^2(1+\cos 2x)\)\(=\displaystyle -2r^2\cos^2 x<0\)
よって,\(\displaystyle \frac{\pi}{4}\leqq x \leqq \frac{\pi}{2}\)の時,\(S(x)\)は常に減少関数である.
以上より,\(\displaystyle \cos 2a=\frac{1+ \sqrt{17}}{8}\)