中級者
数学Ⅰ:方程式と不等式
-
ヒント:1.最大値,最小値を求める=範囲を求めるということである. 範囲を求める方法として,①不等式を作る.②関数をグラフ(図形と方程式)で表してみる.③関数の増減表を作る.④最大値or最小値なら相加相乗関係.(⑤ベクトルで解く.)などが存在する. なお,解と係数の関係を使う時,判別式を使って範囲を確保する必要がある.これは盲点になることがあるので注意.
問題
①実数\(x,y\)が\(x+y=2\)および\(x\geqq0,y\geqq0\)を満たすとき,
(1)\(xy\)の最大値と最小値を求めよ.
(2)\(x^{2}y^{2}+x^{2}+y^{2}-xy\)の最大値と最小値を求めよ.(オリジナル:類 同志社)
(1)の考え方
(1)を見たときどうするか?最大値,最小値を求めよということは範囲を聞かれているということである.(←★)
また式は簡略化するために文字を減らして考えてみよう.
(1)\(y\)を消去する.\(y=2−x\)…① \(x\geqq0,y\geqq0 ⇔ x\geqq0,2−x\geqq0 ⇔ 0\leqq x \leqq2\)…②
一方,\(xy=x(2−x)=-\left(x-1\right)^{2}+1\)…③(二次関数の考え方に帰着する.)
以上より
\(x=1\)のとき,\(MAX~1\),\(x=0,1\)のとき,\(MIN~0\)
(2)の考え方
(1)は何のためにあるのか?それを考えてみると対称式という考えがある.それは,\(x,y\)の式において,\(x\)と\(y\)を入れかえても同じ式になるとき,\(x+y\)と\(xy\)の式で表せるということである.解法のプロセスとしては,(1)はなぜあるのか?それを使うとしたら何か?を考えればよい.
(2)\(x+y=X=2\), \(xy=Y\)とおくと,
\(x^{2}y^{2}+x^{2}+y^{2}-xy\)\(=(x+y)^{2}+x{}^{2}y^{2}-3xy\)\(=Y^{2}-3Y+4\)\(=\left(Y-\displaystyle \frac{3}{2}\right)^{2}+\displaystyle \frac{7}{4}\) ←\(Y\)だけの関数になった!\(Y\)以外は考えず,二次関数を考えろ.
ここで,(1)から \(0\displaystyle \leqq xy=Y\leqq1\) なので,
\(xy=0\)のとき,\(MAX~4\)
\(xy=1\)のとき,\(MIN~2\)
方程式 \(3x^{2}+2xy+3y^{2}=8\)を満たす\(x,y\)に対して,\(u=x+y,~v=xy\)とおく.
(1)\(u^{2}-4v\geqq 0\)を示せ.
(2)\(u,v\)の間に成り立つ等式を求めよ.
(3)\(k=u+v\)がとる値の範囲を求めよ.(九州産大)
解答
(1)\(x,y\)は実数の範囲である.ここで,\(x,y\)を実数解にもつ方程式は,\(t^{2}-(x+y)t+xy=0\)\(\Leftrightarrow\) \(t^{2}-ut+v=0\)とおける.この方程式が実数解を持つ条件は判別式\(D=u^{2}-4v\geqq 0\)
(2)\(3x^{2}+2xy+3y^{2}=8\) \(\Leftrightarrow\) \(3(x+y)^{2}-4xy=8\)なので,\(u=x+y,v=xy\)で変換すると,\(3u^{2}-4v=8\)
(3)条件は\(3u^{2}-4v=8\cdots①\), \(u^{2}-4v\geqq 0\cdots②\),\(k=u+v\cdots③\)
①,②から\(v\)を消去すると,\(u^{2}-4\leqq 0\)\(\Leftrightarrow\)\(-2\leqq u\leqq 2\)…④(同値関係は①②⇔①④)
①,③から\(v\)を消去して\(k\)について解くと,\(k=\displaystyle \frac{3}{4}u^{2}+u-2=\frac{3}{4}\left(u+\frac{2}{3}\right)^{2}-\frac{7}{3}…⑤\) (同値関係は①③⇔①⑤)
④,⑤から\(k\)の最大値は\(u=2\)で\(k=3\),\(k\)の最小値は\(u=-\displaystyle \frac{2}{3}\)で\(k=-\displaystyle \frac{7}{3}\)
よって答えは\(-\displaystyle \frac{7}{3}\leqq k\leqq 3\)
別解 (3)図形と方程式として問題を解く.
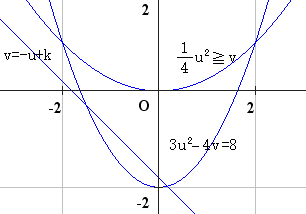
1,\(k\)の最大値は\((u,v)=(2,1)\)を通る時. 2,\(k\)の最小値は\(3u^{2}-4v=8\)と\(v=−u+k\)が接するときである.
1は\(k=3\), 2は\(k=-\displaystyle \frac{7}{3}\)
よって\(-\displaystyle \frac{7}{3}\leqq k\leqq 3\)