上級者
数Ⅱ:図形と方程式
-
ヒント:\(x,y\)の対称式の時は,\(x+y,xy\)の形で式をまとめることができる.この時,文字を置き換えする時は,解と係数の関係を考えて,判別式から範囲を求める必要がある.
問題
実数\(x,y\)が\(4x^2y^2+2xy+x^2+y^2\leqq 3\)を満たしながら変化するとする.
\(m>0\)の時,\(xy-m(x+y)\)の最大値を\(m\)を用いて表せ.
解答
\(s=x+y\),\(t=xy\)と置くと,
実数\(x,y\)を解に持つ2次方程式は次のとおり示させる.
\((u-x)(u-y)\)\(=u^2-su+t=0\)
この方程式が実数を持つため,判別式\(D=s^2-4t \geqq 0\cdots\)①
次に\(4x^2 y^2+2xy+x^2+y^2\leqq 3\)を式変形すると,
\(s^2+4t^2 \leqq 3\cdots\)②
①,②の範囲をグラフに描くと次の通り.
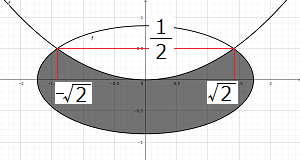
\(k=xy-m(x+y)=-ms+t\)と置き,式変形すると,
\(t=ms+k\cdots\)③
最大値は楕円\(s^2+4t^2 \leqq 3\)の接線となるか,\((s,t)\)\(=\displaystyle \left(-\sqrt{2},\frac{1}{2}\right)\)を通る直線である.
点\((s,t)\)の楕円の傾きは\(\displaystyle -\frac{s}{4t}\)となる.ここで,\((s,t)\)\(=\displaystyle \left(-\sqrt{2},\frac{1}{2}\right)\)における接線は\(\displaystyle t=\frac{\sqrt{2}}{2}(s+\sqrt{2})+\frac{1}{2}\) \(\Leftrightarrow\) \(\displaystyle t=\frac{\sqrt{2}}{2}s+\frac{3}{2}\)
よって,\(\displaystyle m<\frac{\sqrt{2}}{2}\)の時,③が\((s,t)\)\(=\displaystyle \left(-\sqrt{2},\frac{1}{2}\right)\)を通る場合が最大値となる.よって,\(\displaystyle k=\sqrt{2}m+\frac{1}{2}\)
\(\displaystyle m\geqq \frac{\sqrt{2}}{2}\)の時,楕円\(s^2+4t^2 \leqq 3\)の接線が最大値となる.
よって,\(\displaystyle m=-\frac{s}{4t}\)で,③が\((s,t)\)を通る場合で,\(s^2+4t^2=3\)となる.
これより計算すると,\(\displaystyle k=\frac{\sqrt{3}}{2}\sqrt{1+4m^2}\)
よって,答えは
\(\displaystyle m\geqq \frac{\sqrt{2}}{2}\)の時,最大値\(\displaystyle \frac{\sqrt{3}}{2}\sqrt{1+4m^2}\)
\(\displaystyle m<\frac{\sqrt{2}}{2}\)の時,最大値\(\displaystyle \sqrt{2}m+\frac{1}{2}\)
参考入試問題
実数\(x,y\)が\(x^2+y^2 \leqq 1\)を満たしながら変化するとする.
(1) \(s=x+y\),\(t=xy\)とするとき,点\((s,t)\)の動く範囲を\(st\)平面上に図示せよ.
(2) 負でない定数\(m \geqq 0\)をとるとき,\(xy+m(x+y)\)の最大値,最小値を\(m\)を用いて表せ.(2005 東工大)
解答
(1)
実数\(x,y\)を解に持つ2次方程式は次のとおり示させる.
\((u-x)(u-y)\)\(=u^2-su+t=0\)
この方程式が実数を持つため,判別式\(D=s^2-4t \geqq 0\cdots\)①
次に\(x^2+y^2 \leqq 1\)を式変形すると,
\(s^2-2t \leqq 1\cdots\)②
①,②の範囲をグラフに描くと次の通り.
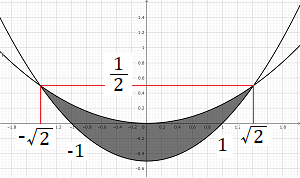
(2)
\(k=xy+m(x+y)=ms+t\)と置き,式変形すると,
\(t=-ms+k\cdots\)③
(1)で求めた範囲(①②)と③の交点を考えると,
\(m \geqq 0\)なので,最大値は\((s,t)\)\(=\displaystyle \left(\sqrt{2},\frac{1}{2}\right)\)を通る場合である.
よって,③に代入して,\(\displaystyle k=\sqrt{2}m+\frac{1}{2}\)
最小値は放物線\(\displaystyle t=\frac{s^2}{2}-\frac{1}{2}\)の接線となるか,\((s,t)\)\(=\displaystyle \left(-\sqrt{2},\frac{1}{2}\right)\)である.
ここで,\((s,t)\)\(=\displaystyle \left(-\sqrt{2},\frac{1}{2}\right)\)における接線は\(\displaystyle t=-\sqrt{2}(s+\sqrt{2})+\frac{1}{2}\) \(\Leftrightarrow\) \(\displaystyle t=-\sqrt{2}s-\frac{3}{2}\)
これより,\(m\geqq \sqrt{2}\)の時は,\((s,t)\)\(=\displaystyle \left(-\sqrt{2},\frac{1}{2}\right)\)を通る場合が最小値となる.
③に代入して,\(\displaystyle k=\frac{1}{2}+m(-\sqrt{2})\)\(\displaystyle =-\sqrt{2}m+\frac{1}{2}\)
一方で,\(m< \sqrt{2}\)の時は,放物線\(\displaystyle t=\frac{s^2}{2}-\frac{1}{2}\)の接線が最小値となる.
よって,点\((s,t)\)\(=\displaystyle \left(s,\frac{s^2}{2}-\frac{1}{2}\right)\)を傾き\(m=s\)の接線を通るので,③に点の値と,傾き\(m=s\)を代入すると,\(\displaystyle k=-\frac{m^2}{2}-\frac{1}{2}\)
以上まとめると,
最大値は\(\displaystyle \sqrt{2}m+\frac{1}{2}\)
最小値は,\(m\geqq \sqrt{2}\)の時は,\(\displaystyle -\sqrt{2}m+\frac{1}{2}\)
\(m< \sqrt{2}\)の時は,\(\displaystyle -\frac{m^2}{2}-\frac{1}{2}\)