上級者
図形問題
-
ヒント：とにかく条件を書き下していこう．相似や合同を発見して等式を作ろう．
問題
面積1の正方形を中心を通るように折り曲げる．重なる部分の面積\(S\)の範囲を求めよ．（類 東工大2001 オリジナル）
この問題を解くときに三角関数を使う．この場合，式変形の中で\(\sin \theta,~\sin 2\theta,~\cos\theta,~\cos 2\theta,~\tan 2\theta\)が一つの式に入ることもあり，かなり煩雑になるが，私の経験的にすべて\(\tan\theta\)に置き換えると，計算がスムーズにいくことがある．
解答
一辺\(2a(=1)\)として，図を次のように考える．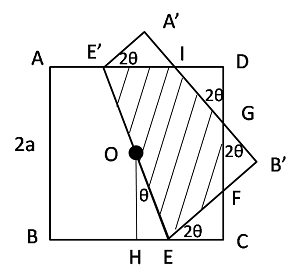
まず角度について，\(\angle HOE＝\theta\)と置く．
\(\angle OEH=90^{\circ}-\theta\)
折り曲げていることから，
\(\angle OEH=\angle OEF\)
よって，\(\angle CEF=180^{\circ}-\angle BEF=2\theta\)
次に，\(\angle AE'E=180^{\circ}-\angle OEH\)
また，\(\angle A'E'I=\angle A'E'E-\angle IE'E=\angle A'E'E-(180^{\circ}-\angle AE'E)\)
折り曲げていることから，
\(\angle A'E'E=\angle AE'E\)
よって，\(\angle A'E'I=2\theta\)
また，\(\angle A'IE'=\angle DIG,~ \angle A'E'I=\angle GDI=90^{\circ}\)
よって，\(\angle DGI=\angle A'E'I=2\theta\)
次に，長さについて，
\(EH=a\tan\theta\)
よって，\(CE=a-a\tan\theta=a(1-\tan\theta)\)
\(CF=CE\tan 2\theta=a(1-\tan\theta)\tan 2\theta\)
ここで，\(\tan 2\theta=\displaystyle \frac{2\tan \theta}{1-\tan^{2}\theta}\)を代入すると，
\(CF=\displaystyle \frac{2a\tan \theta}{1+\tan\theta}\)
中心を通ることから，
\(AE'=CE=a(1-\tan\theta)\)
折り曲げていることから，
\(A'E'=AE'\)
よって，\(IE'=\displaystyle \frac{A'E'}{\cos 2\theta}=\displaystyle \frac{CE}{\cos 2\theta}=\displaystyle a\frac{(1-\tan \theta)}{\cos 2\theta}\)
ここで，\(\cos 2\theta=\displaystyle \frac{1-\tan \theta}{1+\tan \theta}\)より，
\(IE’=\displaystyle a\frac{1+\tan^{2}\theta}{1+\tan \theta}\)
さらに，\(DE'=AD-AE'=2a-a(1-\tan\theta)=a(1+\tan\theta)\)
また，\(DI=DE'-IE'=a(1+\tan\theta)-\displaystyle a\frac{1+\tan^{2}\theta}{1+\tan \theta}=\displaystyle \frac{2a\tan \theta}{1+ \tan \theta}\)
\(DG=\displaystyle \frac{DI}{\tan 2\theta}=a(1-\tan \theta)\)
面積\(S=□ECDE'-△CEF-△DGI\)
\(=\displaystyle \frac{1}{2}\{(CE+DE')\times 2a)-(CE\times CF)-(DG\times DI)\}\)
\(=\displaystyle \frac{1}{2}\{4a^{2}-4a^{2}\frac{\tan\theta(1-\tan\theta)}{1+\tan\theta}\}=\frac{2a^{2}(1+\tan^{2}\theta)}{1+\tan\theta}\)
ここで，\(\displaystyle 1+\tan^{2}\theta=\displaystyle \frac{1}{\cos^{2}\theta}\)を使って，さらに次のように式変形する．
面積\(S=\displaystyle \frac{2a^{2}}{\cos^{2}\theta+\sin\theta\cos\theta}\)
また，\(\cos^{2}\theta=\displaystyle \frac{1+\cos 2\theta}{2},~\sin\theta\cos\theta=\displaystyle \frac{\sin 2\theta}{2}\)を代入して式変形すると，
面積\(S=\displaystyle \frac{4a^{2}}{1+\cos 2\theta+\sin 2\theta}=\displaystyle \frac{4a^{2}}{1+\sqrt2\sin(2\theta+\frac{\pi}{4})}\)
ここで対称性より，\(0\leqq\theta\leqq\displaystyle \frac{\pi}{4}\)を考えればよい．
よって，\(4a^2(\sqrt2-1) \leqq S \leqq 2a^{2}\Leftrightarrow \sqrt2-1 \leqq S \leqq \displaystyle \frac{1}{2}\)
★他に，\(\tan\theta\)で微分して，増減表から求める方法がある．
もし最小値だけ求めるなら，相加相乗平均が使える．
面積\(S=2a^{2}\left((1+\tan\theta)+\displaystyle \frac{2}{1+\tan\theta}-2\right) \geqq 2a^2(2\sqrt2-2)=4a^2(\sqrt2-1)\)
★対称性などを考えると，\(\angle EOG=90^{\circ},~\angle OEG=45^{\circ}\)より，\(OE=OG\) ．また，\(\angle FEG= \angle FGE=45-\theta\)より，\(FE=FG\)となる．
ここを起点として，\(S=2\times(△OEG+△EFG)\)から求めることもできる．試しに計算してみよう．
参考入試問題
②面積1の\(△ABC\)において，辺\(AB\)上に1点\(P\)をとり\(P\)を通り辺\(BC\)に平行な直線と辺\(AC\)の交点を\(Q\)とする．さらに線分\(PQ\)の中点に関して\(A\)と対称な点を\(R\)とする．点\(P\)が辺\(AB\)上を動くとき\(△ABC\)と\(△PQR\)の共通部分の面積の最大値を求めよ．（京都大）
考え方 少し分かりにくいので，図を描いてみよう．
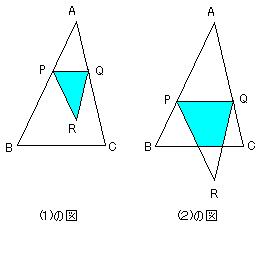\(P\)が\(AB\)上を動くのだから，\(AP=t\)とおいて\(t\)を動かしてみて面積\(S\)がどう変わるのか考えてみよう．
\(AB=a\)とおく．
（１）のときつまり\(0\displaystyle \leqq t\leqq\frac{a}{2}\)のとき\(S=△PQR=△PQA\) ここで\(△APQ∽△ABC\)で辺の比\(t:a\)はとって面積比は\(t^{2}:a^{2}\)となる．
\(∴t^{2}:a^{2}=S:1\displaystyle \Leftrightarrow S=\frac{t^{2}}{a^{2}}\)
（２）のときつまりの\(\displaystyle \frac{a}{2}<t\leqq a\)とき\(BC\)と\(PR,QR\)の交点を\(D,E\)とおく．すると，\(PB=QE\)となるため
\(QR=a−t, ER=t−(a−t)=2t−a\)
ここで\(S=△RPQ−△RDE\)より\((a-t)^{2}-(2t-a)^{2}:a^{2}=S:1\displaystyle \Leftrightarrow S=\frac{-3t^{2}+4ta}{a^{2}}=-\frac{3}{a^{2}}\left(t-\frac{2}{3}a\right)^{2}+\frac{1}{3}\)
ここで，(１)の最大値は\(t=\displaystyle \frac{a}{2}\)で\(S=\displaystyle \frac{1}{4}\)
(２)の最大値は\(t=\displaystyle \frac{2}{3}a\)で\(S=\displaystyle \frac{1}{3}\)
よって面積の最大値は\(\displaystyle \frac{1}{3}\)
(実際は\(a=1\)などとしても面積には影響はないからおくのは何でもよい．)
※分かりにくそうな問題にはどうすればいいのか？
図が描けそうだったら図を描く．そして，頭の中で，動かしてみる．変数をおけたら注意しておく．図がかけない場合は変数は何か？定数は何か？分からない値は文字でおく．などをやるしかない．とにかく今までやってきたことをすべて関連付けるような勉強をしていかないとこのような力はつきにくい．