上級者
図形問題
-
ヒント:図形問題は適切な文字の設定とそれを数式化を行う必要がある.数式の解き方は様々あるので,そこは問題を解きつつ慣れていこう.
問題
正四面体\(ABCD\)の\(AB\)上で点\(P\)が動くとき,\(\cos \angle CPD\)の最小値を求めよ.(オリジナル)
①余弦定理を多用する方法と②ベクトルを使って解く方法があるが,ベクトルの解き方は慣れると計算が楽になるので,今回はベクトルで解いてみる.
解答
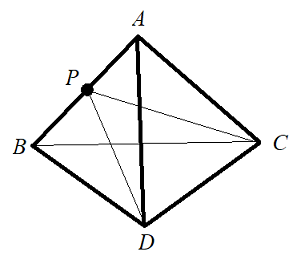
辺の長さを\(a\),\(\angle CPD=\theta,~AP=t\)と置く.
ベクトルの内積の式から,
\(\overrightarrow{CP}\cdot\overrightarrow{DP}=|\overrightarrow{CP}||\overrightarrow{DP}|\cos \theta\)
ここで余弦定理より,
\(|\overrightarrow{CP}|=|\overrightarrow{DP}|=\sqrt{a^{2}+(at)^2-2\cdot a\cdot at\cdot \cos\theta}\)
\(=a\sqrt{(t^2-t+1)}\)
また,\(\overrightarrow{CP}=\overrightarrow{AP}-\overrightarrow{AC}\) ←後ろ\(P\)から前\(C\)を引く
\(\overrightarrow{DP}=\overrightarrow{AP}-\overrightarrow{AD}\) より,
\(\overrightarrow{CP}\cdot\overrightarrow{DP}=|\overrightarrow{AP}|^{2}-\overrightarrow{AP}\cdot\overrightarrow{AC}-\overrightarrow{AP}\cdot\overrightarrow{AD}-\overrightarrow{AC}\cdot\overrightarrow{AD}\)
\(=(at)^{2}-a\cdot at\cdot \cos 60^{\circ}-a\cdot at\cdot \cos 60^{\circ}+a\cdot a\cdot \cos 60^{\circ}\)
\(=\displaystyle a^{2}\left(t^{2}-t+\frac{1}{2}\right)\)
よって,\(\displaystyle \cos \theta=\frac{t^{2}-t+\frac{1}{2}}{t^{2}-t+1}\)
ここで,\(\cos \theta=k\)と置き,\(k\)の範囲を考える.
式変形すると,
\((1-k)t^{2}-(1-k)t+\displaystyle \frac{1}{2}-k=0\)
ここで,\(f(t)=(1-k)t^{2}-(1-k)t+\displaystyle \frac{1}{2}-k\)とすると,
二次関数\(f(t)\)が解を持つような\(k\)の範囲を考えればよい.
ここで,\(k<1\)より,\(f(t)\)は下に凸の関数である.
また\(0\leqq t \leqq 1\)で,軸は\(\displaystyle \frac{1}{2}\)なので,
\(0\leqq t \leqq 1\)で解を2つもつ条件を考えればよい.
(グラフを考えればわかると思うが,)条件は,
\(f(0)>0\) かつ \(f(1)>0\) かつ 最小値\(\geqq 0\) (判別式\(D\geqq 0\))
⇔ \(\displaystyle \frac{1}{2}-k\geqq 0\) かつ \(D=(1-k)(-1+3k)\geqq0\)
\(k<1\)を考慮して,\(\displaystyle \frac{1}{3}\leqq k \leqq \frac{1}{2}\)
\(\cos \angle CPD\)の最小値は\(\displaystyle \frac{1}{3}\)
参考入試問題
②一辺の長さが1の正四面体\(ABCD\)において,\(P\)を辺\(AB\)の中点とし,点\(Q\)が辺\(AC\)上を動くとする.このとき, \(\cos∠PDQ\)の最大値を求めよ.(2015 京都大)
\(\cos∠PDQ=\displaystyle \frac{-t+3}{2\sqrt{3}\sqrt{t^{2}-t+1}}\)
これを微分して増減表を書くと,最大値は\(t=\displaystyle \frac{1}{3}\)で\(\cos∠PDQ=\displaystyle \frac{\sqrt{7}}{3}\)