上級者
図形問題
-
ヒント:1.図形の問題は角度と長さが問題となってくるので,それをしっかり文字で置くようにする.それから図を書いておくと関係が一目でわかるので必ず書くこと.
2.それぞれの問題に応じて条件(関係)などを書きつくせ.(ここでは図形なので角度長さについて書きつくす).そしてその条件のもとで問題を解く.
問題
\(AB=AC\)のとき,\(△DEF\)の面積を\(S'\),\(△ABC\)の面積を\(S\)とすると,\(\displaystyle \frac{S'}{S}\)の範囲をあらわせ.(オリジナル)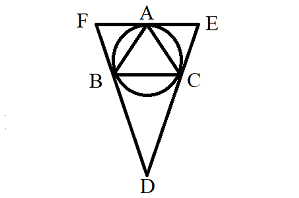
もし,元の問題文で解けない時は,次の過程を確認しながら解いてみよう.
①\(△ABC\)について,\(∠BAC=\alpha\)と,\(∠ABC=\beta\)おいて,\(\alpha,~\beta\)の関係を求めよ.
②\(AE=x\),\(BD=y\)とおいて\(x,~y,~\alpha,~\beta\)を使って\(△DEF\)の面積\(S'\)と\(△ABC\)の\(S\)をあらわせ.
③\(△DEF\)の面積\(S'\)は\(△ABC\)の\(S\)の何倍か?\(\tan\)と\(\beta\)であらわせ.
④何倍が最小値となるか?答えよ.
解説

\(∠BAC=\alpha\),\(∠ABC=\beta\),\(AE=x\),\(BD=y\)とおくと図のようになる.
(∵\(AB=AC\),円に接する時の長さの関係)
\(△ABC\)の\(S=ABAC\displaystyle \frac{\sin\alpha}{2}\)\(=2x^{2}\cos^{2}\beta \sin\alpha\)(∵\(AB=AC=2x\cos\beta\))
また,\(BC=2y\cos\alpha\),\(△ABC∽△EAC\)より,\(AC:BC=EC:AC\)
∴\(BC=4x\cos^{2}\beta\)
∴\(y=\displaystyle \frac{2x\cos^{2}\beta}{\cos\alpha}\)\(=-\displaystyle \frac{2x\cos^{2}\beta}{\cos2\beta}\)
(∵\(\cos\alpha=\cos(180^{\circ}−2\beta)=−\cos 2\beta\))
\(△DEF\)の\(S'=EDEF\displaystyle \frac{\sin\alpha}{2}\)\(=-\displaystyle \frac{x^{2}\sin\alpha(2\cos^{2}\beta-\cos2\beta)}{\cos2\beta}\)
以上から\(\cos2\beta=2\cos^{2}\beta-1\),\(\tan^{2}\displaystyle \beta+1=\frac{1}{\cos^{2}\beta}\)を用いて整理すれば,
\(\displaystyle \frac{S'}{S}=\frac{(\tan^{2}\beta+1)^{2}}{2(\tan^{2}\beta-1)}\)
次に範囲を求める.
\(180^{\circ}=2\beta+\alpha\),\(2\alpha<180^{\circ}\)から,\(45^{\circ}<\beta<90^{\circ}\)
ここで\(\tan^{2}\beta=t\)とおく.(\(t \geqq 1)\)
また,\(\displaystyle \frac{S'}{S}=k\)(\(k>0\))とおく.
これを変形させると,\((t-k+1)^{2}-k^{2}+s4k=0\)
ここで左辺\(=f(t)\)とおく.
(1)\(k−1<1\)のとき
\(f(1)<0\)\(\Leftrightarrow\)\(4<0\)
これは不適.
(2)\(k−1\geqq 1\)のとき
\(f(t)\)の最小値\(\leqq 0\)\(\Leftrightarrow\)\(-k^{2}+4k\leqq 0\)\(\Leftrightarrow\)\(k\leqq 0,k\geqq 4\)
以上より,\(\displaystyle \frac{S'}{S}≧4\)
最小値を求めよという問題なら一番簡単な求め方は?
\(\tan^{2}\beta=t\)とおいて,\(\displaystyle \frac{S'}{S}=\frac{(t+1)^{2}}{2(t-1)}\)とすると,分母が分子の2倍乗なら感覚として相加相乗が使えるのではないかと考えてください.実際にやってみると,
\(\displaystyle \frac{S'}{S}=\frac{(t+1)^{2}}{2(t-1)}\)\(=\displaystyle \frac{1}{2}(t+3+\frac{4}{t-1})=\frac{1}{2}\{(t-1)+\frac{4}{t-1}\}+2\geqq 4\)
等号成立は\((t-1)^{2}=4\) つまり,\(t=3\)のとき (\(t \geqq 1\))
注意:最大値,最小値を求めよ,という時は相加相乗を使ってもよいが,範囲を聞かれているときは,相加相乗を使わないでください.なぜなら,あくまでも一番小さい値としてこれ以上ですよということで,それより大きな値は実際どこまで取るのかはわからないからです.