上級者
図形問題
-
ヒント:1.図形の問題は角度と長さが問題となってくるので,それをしっかり文字で置くようにする.それから図を書いておくと関係が一目でわかるので必ず書くこと.
2.それぞれの問題に応じて条件(関係)などを書きつくせ.(ここでは図形なので角度長さについて書きつくす).そしてその条件のもとで問題を解く.
問題
二等辺三角形の中に半径\(r\)の内接円が存在する.
(1)二等辺三角形の面積が最小となる時,三角形の面積を\(r\)を用いて表せ.
(2)二等辺三角形の辺の長さが最小となる時,辺の長さを\(r\)を用いて表せ.(オリジナル)
解答
各辺を図のようにおく.\(AO=x\),\(CD=CE=y\)
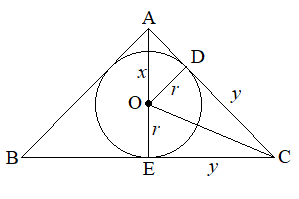
図のように角度\(\angle BAE\)\(=\angle CAE=a\) \(\displaystyle \left(0<a<\frac{\pi}{2}\right)\)とすると,
\(x\)\(=\displaystyle \frac{r}{\sin a}\)
\(y\)\(=\displaystyle r\tan a \left(1+\frac{1}{\sin a}\right)\)
(1)
これより,二等辺三角形の面積\(S\)は
\(S\)\(=(x+r)y\)\(=\displaystyle r^2\tan a\left(\frac{1}{\sin a}+1\right)^2\)
ここで,\(\displaystyle \tan \frac{a}{2}=t\)と置くと,
\(S\)\(=\displaystyle r^2\frac{(t+1)^3}{2t(1-t)}\)
次に,\(t\)で微分すると,
\(S'\)\(=\displaystyle \frac{(t+1)^2(t^2-4t+1)}{2(1-t)^2 t^2}\) \((0<t<1)\)
よって,\(S'=0\)となる\(t\)は\(t=2-\sqrt{3}\)
この時の\(S\)は\(S\)\(=3\sqrt{3}r^2\)
増減表は次の通りで,求める面積は\(3\sqrt{3}r^2\)
\begin{array}{c|c|c|c|c|c}
x & 0 & \cdots & 2-\sqrt{3} & \cdots & 1 \\ \hline
y'& -\infty & - & 0 & + & +\infty \\ \hline
y & +\infty &\searrow& 3\sqrt{3} &\nearrow& +\infty \\ \hline
\end{array}
(2)
二等辺三角形の長さ\(L\)は
\(L\)\(=2\times (x\cos a+2y)\)\(=\displaystyle 2r\left(\frac{1}{\tan a}+2\tan a\left(\frac{1}{\sin a}+1\right)\right)\)
ここで,\(\displaystyle \tan \frac{a}{2}=t\)と置くと,
\(L\)\(=\displaystyle r\frac{(t+1)^3}{t(1-t)}\)
これは(1)と同じで,\(t=2-\sqrt{3}\)で,求める長さは\(6\sqrt{3}r\)
※答えは正三角形となる.