中級者
図形問題
-
ヒント:図形の場合には線や同じ角度を書いていくことが大事である.そこからどのように式に持っていくかがポイント.
問題
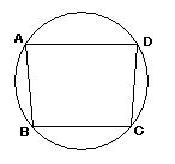
図において,\(AD//BC,~ AD=5,~ AB=BC=CD,~ \displaystyle \cos\angle ACD=\frac{9}{16}\)のとき\(AC\)の長さを求めよ.(オリジナル)
解答
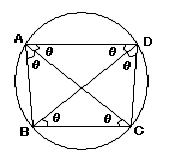
\(∠BAC=\theta\)とおけば\(∠BDC=\theta\)(同位角) また弧において\(AB=BC=CD\)より
\(∠ADB=∠BAC=∠CAD=\theta\)よって\(∠ACD=\pi−3\theta\)
\(\displaystyle \cos(\pi-3\theta)=\frac{9}{16}\Leftrightarrow\cos 3\theta=-\frac{9}{16}\)
ここで\(\cos 3\theta=4\cos^{3}\theta-3\cos\theta\)から
\(4\displaystyle \cos^{3}\theta-3\cos\theta=-\frac{9}{16}\Leftrightarrow 64\cos^{3}\theta-48\cos\theta+9=0\)
ここで予想される因数は\(\displaystyle \pm\frac{9\text{の公約数}}{64\text{の公約数}}\)で当てはめていくと,\(\displaystyle \cos\theta=\frac{3}{4}\)が当てはまる.
∴\((4\cos\theta-3)(16\cos^{2}\theta+12\cos\theta-3)=0\)
∴\(\displaystyle \cos\theta=\frac{3}{4} \frac{-3\pm\sqrt{21}}{8}\)
ここで,\(0<3\theta<\pi\)より \(0<\displaystyle \theta<\frac{\pi}{3}\) ∴ \(\displaystyle \frac{1}{2}<\cos\theta<1\)
この範囲に当てはまるのは\(\displaystyle \cos\theta=\frac{3}{4}\)のみ.
ここで△ABCにおいて,\(AB=a\)とすれば
\(AC=2AB\displaystyle \cos\theta=\frac{3}{2}a\)
∴△ACDで余弦定理より
\(AD^{2}=AC^{2}+CD^{2}-2AC\times CD\cos\angle ACD\) ⇔ \(25=\displaystyle \frac{9}{4}a^{2}+a^{2}-2\times\frac{3}{2}a\times a\times\frac{9}{16}\) ⇔ \(a=4~(a>0)\)
∴\(AC=\displaystyle \frac{3}{2}a=6\)
※三角関数は計算がうまくでき,すぐにが変形できることが重要.(二倍角,加法,半角など)また,和積,積和公式もよくあるから黄チャートや教科書傍用問題集をやって計算力を鍛えるとよい.