中級者
図形問題
-
ヒント:図形の場合には線や同じ角度を書いていくことが大事である.そこからどのように式に持っていくかがポイント.
問題
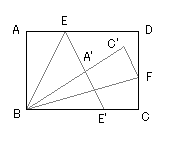
四角形\(ABCD\)を\(BE\)と\(BF\)で折り曲げ,さらに,\(A’B\)を折り目として,\(△BEA’\)を折り曲げると,点\(E\)は\(BC\)上につく.\(AB=3,AD=4\)のとき,\(C’D\)を求めよ.(オリジナル)
解答
\(AB=A'B=3,~BC=BC'=4\)より,\(A'C'=1\)
また,\(\angle ABE=\angle A'BE=\angle A'BE'\),\(\angle ABE'=90^{\circ}\)なので,\(\angle A'BE'=30^{\circ}\)
よって,\(\displaystyle AE=\frac{AB}{\sqrt{3}}=\sqrt{3}\)
また,\(A'E=AE\),\(\angle EA'C'=90^{\circ}\)なので,
三平方の定理より,\(C'E^{2}=A'E^{2}+A'C'^{2}\)
よって,\(C'E=2\)
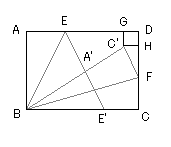
\(\displaystyle A'C'=1,~A'E=\sqrt{3},~C'E=2\)より,
\(\angle A'EC'=30^{\circ}\cdots\)①
また,\(\angle AEB=\angle A'EB=60^{\circ}\)
よって,\(\angle AE'G=60^{\circ}\cdots\)②
①,②より,\(\angle C'EG=30^{\circ}\)
また,\(C'E=2\)より,\(C'G=1,~ EG=\sqrt{3}\)
よって,\(DH=C'G=1\),\(GD=AD-AE-EG=4-2\sqrt{3}\)
三平方の定理より,\(C'D^{2}=GD^{2}+C'G^{2}\)
\(C'D=\sqrt{29-16\sqrt{3}}\)
※\(DH\)と\(GD\)は,\(CF=BC\tan 15^{\circ}\),\(FH=C'F\cos 30^{\circ}\),\(C'H=C'F\sin 30^{\circ}\)からも求めることができる.