MATH

ヒント：基本に忠実に長さを描き，図形を解く定理を思い出しながら何が使えるか考えよう．

問題
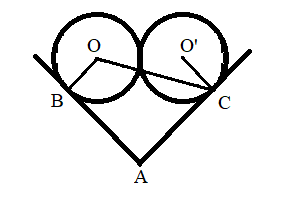
\(\angle ABO\)\(=\angle ACO'\)\(=90^{\circ}\)とする。\(AC=a\)，\(AB=b\)，\(\displaystyle CO=\frac{\sqrt{21}}{3}a\)，\(\displaystyle BO'=\frac{\sqrt{21}}{3}b\)，\(BO=CO'=r\)が成り立つとする．\(r=1\)の時，\(a\)の値を求めよ．


解答
\(O\)と\(O'\)の交点を\(D\)とすると、\(AD\)と円Oと円O'は接する．よって\(AC=AD=AB=a=b\)が成り立つ．次に，\(CD=c\)とおくと，\(△COO'\)において，中線定理より，\(CO^2+CO'^2=2(CD^2+DO^2)\)が成り立つ．これより，\(\displaystyle \frac{7}{3}a^{2}+r^{2}=2(c^{2}+r^{2})\cdots\)①
また，\(CD\)の中点を\(E\)とすると，\(CD\)と\(AO'\)は直交する．ここで，\(△ACO'\)と\(△AEC\)は相似であるため，\(AC:CE=AO':CO'\)が成立する．これより，\(\displaystyle ar=\frac{c}{2}\sqrt{a^{2}+r^{2}}\)
二乗して，\(4a^2r^{2}=c^{2}(r^{2}+a^{2})\cdots\)②
①，②より，\(c\)を消すと，
\(3r^4+20a^2r^2-7a^4=0\) \(\Leftrightarrow\) \((r^2+7a^2)(\sqrt{3}r+a)(\sqrt{3}r-a)=0\)
よって，\(a=\sqrt{3}r=\sqrt{3}\)