MATH

ヒント：図形を各文字に置き換え，代数的に解くと難しい問題ですが，図形的に解くと簡単に解けます．

問題
三角形\(ABC\)に対して，\(AB=c\)，\(BC=a\)，\(CA=b\)，内接円の半径を\(r\)，外接円の半径を\(R\)とする．\(a=2R\)を満たす時，\(\displaystyle k=\frac{R}{r}\)の範囲を求めよ．

解答
〇図形的に解くと…

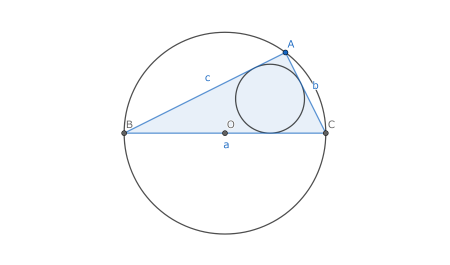
\(a=2R\)，つまり\(BC\)は外接円の直径となる．図に描くと明らかなように，\(\angle A=90^{\circ}\)である．
ここで対称性より，\(b\leqq c\)と考えてよい．
まず，内接円\(r\)が最も小さくなる場合は，明らかに\(b\rightarrow 0\)である．

この時，\(r\rightarrow 0\)であるため，\(k\rightarrow \infty\)である．

また，内接円\(r\)が最も大きくなる場合は，明らかに\(b=c\)である．
この時，\(\angle B=\angle C=45^{\circ}\)であり，\(\displaystyle b=c=\frac{a}{\sqrt{2}}\)である．
ここで三角形の面積\(S\)は内接円の半径\(r\)を使うと，\(\displaystyle S=\frac{1}{2}(a+b+c)r\)
また，\(\angle A=90^{\circ}\)より\(\displaystyle S=\frac{1}{2}bc\)である．
よって，\(\displaystyle \frac{1}{2}(a+b+c)r\)\(=\displaystyle \frac{1}{2}bc\)

ここに\(\displaystyle b=c=\frac{a}{\sqrt{2}}\)を代入して整理すると，\(\displaystyle \frac{a}{r}\)\(=2(1+\sqrt{2})\)
さらに\(a=2R\)を代入して整理すると，\(\displaystyle k=\frac{R}{r}\)\(=1+\sqrt{2}\)
以上より，\(k\geqq 1+\sqrt{2}\)が答えとなる．

〇代数的に解くと…
正弦定理より，\(\displaystyle 2R=\frac{a}{\sin A}\)（\(A\)は角度）
\(a=2R\cdots(1)\)より，\(\sin A=1\)
ここで，\(0<A<180^{\circ}\)より，\(\displaystyle A=90^{\circ}\)
よって，\(a^2=b^2+c^2\cdots(2)\)が成り立つ．
次に三角形\(ABC\)の面積\(S\)は次の2通りで表される．
\(\displaystyle S=\frac{1}{2}(a+b+c)r\)
\(\displaystyle S=\frac{1}{2}bc\)
よって，\((a+b+c)r=bc\cdots(3)\)
また，\(R=kr\cdots(4)\)
(1)(4)より，\(R\)を消去すると，
\(a=2kr\cdots(1)'\)
(1)'(3)より，\(r\)を消去すると，
\((a+b+c)a=2kbc\cdots(3)'\)
(2)で\(a>0\)より，\(a=\sqrt{b^2+c^2}\)を(3)'に代入して整理すると，
\((b+c)\sqrt{b^2+c^2}=2kbc-(b^2+c^2)\)
これをさらに2乗して整理すると，
\(2bc((2k+1)b^2-2k^2bc+(2k+1)c^2)=0\)
ここで，\(b\neq 0\)，\(c\neq 0\)より，
\((2k+1)b^2-2k^2bc+(2k+1)c^2=0\)
ここで，\(f(b)=(2k+1)b^2-2k^2bc+(2k+1)c^2\)と置く．
ここで，\(k>0\)より，
\(\displaystyle f(b)=(2k+1)(b-\frac{k^2}{2k+1}c)^2-\frac{(k+1)^2(k^2-2k-1)}{2k+1}c^2\)
\(b\)の取りうる範囲は\(0<b<a\)であるので，下に凸の二次関数\(f(b)\)において，軸の位置で場合分けをする．

①軸が\(0<\displaystyle \frac{k^2}{2k+1}<a\)である場合，

\(f(b)=0\)が解を持つには，最小値\(\displaystyle -\frac{(k+1)^2 (k^2-2k-1)}{2k+1}c^2\leqq 0\)が条件となる．
これより，\(k>0\)かつ\(k^2-2k-1\leqq 0\)から，\(k\geqq 1+\sqrt{2}\)

②軸が\(\displaystyle \frac{k^2}{2k+1}>a\)である場合，\(f(b)=0\)が解を持つには，\(f(0)\geqq 0\)，\(f(a)\leqq 0\)が条件となる．

ここで，\(f(0)\)と\(f(a)\)の大きさを確認すると，\(f(0)=(2k+1)c^2\geqq 0\)，\(f(a)=(2k+1)a^2\geqq 0\)（\(b=a,c=0\)）となるため，\(f(b)=0\)が解は存在しない．

以上より，\(k\geqq 1+\sqrt{2}\)が答えとなる．