上級者
数学Ⅲ:積分法
-
ヒント:回転体を求める時に複数の関数がある場合は,どちらの関数が優先すべき関数か場合分けが必要である.また,回転体を求める時は,余分な体積を引く必要がある場合があるので,注意が必要である.(媒介変数を使うような関数ではよく現れる)
問題(オリジナル)
\(y=x^2\)と\(y=-2x^2+3x\)で囲まれる領域を\(y=x\)の周りに1回転してできる立体の体積\(V\)を求めよ.
解答
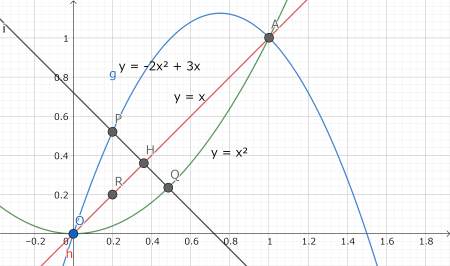
図のようなグラフと点を描く.なお,\(OH⊥PH\),\(OH⊥QH\)である.
ここで点\(P\),点\(Q\)の\(x\)座標を\(a\)と置くと,点\(R(a,a)\),\(P(a,-2a^2+3a)\),\(OR=\sqrt{2}a\)
ここで,\(PR=\sqrt{2}PH=\sqrt{2}RH\)で,\(PR=-2a^2+2a\)
よって,\(PH=\sqrt{2}(-a^2+a)\),\(OH=OR+RH=\sqrt{2}(-a^2+2a)\)
また,\(\displaystyle H(-a^2+2a,-a^2+2a)\)で直線\(PH\)の傾きは-1なので,
\(PH:y=-(x-(-a^2+2a))-(-a^2+2a)\)\(=-x+2(-a^2+2a)\)
ここで,直線\(PH\)と\(y=x^2\)の\(x>0\)以上の交点\(Q\)については,
\(x^2=-x+2(-a^2+2a)\)の方程式を解くと,\(\displaystyle x=\frac{-1+\sqrt{1+8(-a^2+2a)}}{2}\)
これより,\(Q\)と\(H\)の\(x\)座標の差は\(\displaystyle \frac{-1+\sqrt{1+8(-a^2+2a)}}{2}-(-a^2+2a)\)で,この\(\sqrt{2}\)倍が\(QH\)となる.
よって,\(QH=\displaystyle \sqrt{2}\left(\frac{-1+\sqrt{1+8(-a^2+2a)}}{2}-(-a^2+2a)\right)\)
ここで,\(PH\)と\(QH\)の大きさによって,\(y=x^2\)の回転体か\(y=-2x^2+3x\)の回転体のいずれかを選択する必要がある.
ここで,\(PH=QH\)\(\Leftrightarrow\)\(\displaystyle \sqrt{2}(-a^2+a)=\sqrt{2}\left(\frac{-1+\sqrt{1+8(-a^2+2a)}}{2}-(-a^2+2a)\right)\)\(\Leftrightarrow\)\(\sqrt{-8a^2+16a+1}=-4a^2+6a+1\)
ここで,両辺2乗して整理すると,\(a(a-1)(4a^2-8a+1)=0\)
\(0\leqq a \leqq 1\)なので,\(\displaystyle a=0,1,1-\frac{\sqrt{3}}{2}\)
ここで,\(\displaystyle 0\leqq a \leqq 1-\frac{\sqrt{3}}{2}\)では\(PH \leqq QH\)
ここで,\(\displaystyle 1-\frac{\sqrt{3}}{2} \leqq a \leqq 1\)では\(PH \geqq QH\)
ここで\(PH\)の回転体を求める時に,余分な体積を引く必要がある場合を考える必要がある.つまり,\(y=-x+d\)と\(y=-2x^2+3x\)を接する時に\(x=\alpha<1\)で接する場合は,積分区間を\(x=\alpha\)前後で分けて,\(x \leqq \alpha\)の回転体の体積から\(x \geqq \alpha\)の回転体の体積を引く必要がある.
ここで,\(y=-x+d\)と\(y=-2x^2+3x\)が接する時は,\(d=2\)で,\(x=1\)となる.これより,余分な体積を引く必要はない.
以上より,求める回転体の体積\(V\)は,\(OH=t\)と置くと,\(0 \leqq t \leqq \sqrt{2}\)の範囲で,
\(V\)\(=\displaystyle \pi\int_{0}^{t_{1}}{QH}^2 dt\)\(+\displaystyle \pi\int_{t_{1}}^{\sqrt{2}}{PH}^2 dt\)
ここで,\(dt=2\sqrt{2}(-a+1)da\),\(t:0\rightarrow t_{1} \rightarrow \sqrt{2}\)で\(\displaystyle a:0\rightarrow 1-\frac{\sqrt{3}}{2} \rightarrow 1\)
\(V\)\(=\displaystyle 2\sqrt{2}\pi\int_{0}^{1-\frac{\sqrt{3}}{2}}\left(\sqrt{2}\left(\frac{-1+\sqrt{1+8(-a^2+2a)}}{2}-(-a^2+2a)\right)\right)^2 (-a+1)da\)\(+\displaystyle 2\sqrt{2}\pi\int_{1-\frac{\sqrt{3}}{2}}^{1}{(\sqrt{2}(-a^2+a))}^2 (-a+1)da\)
ここで,\(V_{1}\)\(=\displaystyle 2\sqrt{2}\pi\int_{0}^{1-\frac{\sqrt{3}}{2}}\left(\sqrt{2}\left(\frac{-1+\sqrt{1+8(-a^2+2a)}}{2}-(-a^2+2a)\right)\right)^2 (-a+1)da\)について,\(x=\sqrt{1+8(-a^2+2a)}\)と置くと,
\(a:0\rightarrow 1-\frac{\sqrt{3}}{2}\)で\(\displaystyle x:1\rightarrow \sqrt{3}\)
また\(x^2=1+8(-a^2+2a)\)で,\(\displaystyle 2x\frac{dx}{da}=16(-a+1)\)
よって,\(V_{1}\)\(=\displaystyle 4\sqrt{2}\pi\int_{1}^{\sqrt{3}}\left(\frac{-1+x}{2}-\frac{x^2-1}{8}\right)^2 \frac{x}{8}dx\)\(=\displaystyle \frac{\sqrt{2}}{128}\pi\int_{1}^{\sqrt{3}}x(-x^2+4x-3)^2 dx\)\(=\displaystyle \frac{\sqrt{2}}{128}\pi\left[\frac{x^6}{6}-\frac{8x^5}{5}+\frac{11x^4}{2}-8x^3+\frac{9x^2}{2}\right]_{1}^{\sqrt{3}}\)\(=\displaystyle \frac{\sqrt{2}}{480}\pi(251-144\sqrt{3})\)
\(V_{2}\)\(=\displaystyle 2\sqrt{2}\pi\int_{1-\frac{\sqrt{3}}{2}}^{1}{(\sqrt{2}(-a^2+a))}^2 (-a+1)da\)\(=\displaystyle 4\sqrt{2}\pi\int_{1-\frac{\sqrt{3}}{2}}^{1}(-a^5+3a^4-3a^3+a^2)da\)\(=\displaystyle 4\sqrt{2}\pi\left[-\frac{a^6}{6}+\frac{3a^5}{5}-\frac{3a^4}{4}+\frac{a^3}{3}\right]_{1-\frac{\sqrt{3}}{2}}^{1}\)\(\displaystyle =\frac{9\sqrt{2}}{160}\pi(15-8\sqrt{3})\)
よって,\(V\)\(=V_{1}+V_{2}\)\(=\displaystyle \frac{\sqrt{2}}{60}\pi(82-45\sqrt{3})\)