上級者
数学Ⅲ:積分法
-
ヒント:媒介変数を用いた面積の時は方向などに注意すること.
問題
一辺が\(a\)の正方形\(ABCD\)の中に,一辺が\(a\)の正三角形\(EFG\)の各頂点を中心に,異なる二頂点を半径\(a\)の円弧で結んでできる図形であるルーローの三角形が存在する.このルーロの三角形は,常に頂点か円弧が正方形\(ABCD\)の辺に接しながら,正方形\(ABCD\)の内部を動いている.この場合,ルーローの三角形が動く範囲の面積を求めよ.(オリジナル)
解答
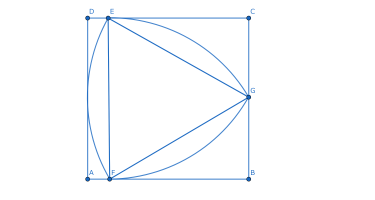
図のような配置を考えた時,\(\angle BFG=\theta\)と置く.
ここで点\(E\)の軌跡を考える場合,\(E\)が\(CD\)を離れる瞬間の点を\(E'\),\(DA\)上に接する瞬間の点を\(E''\)とする.この時の\(\theta\)の範囲は,\(\displaystyle \frac{\pi}{6} \leqq \theta \leqq \frac{\pi}{3}\)である.また,図形\(DE'E''\)(\(E'E''\)は\(E\)の軌跡)の面積\(S_{1}\)とすると,図形の対称性より,求める面積\(S\)は,\(a^{2}-4S_{1}\)となる.
ここで,\(A\)の座標を\(A(0,0)\)とすると,\(F(a-a\cos\theta,0)\),\(\displaystyle \angle AFE=\frac{2\pi}{3}-\theta\)であることから,\(E(x_{E},y_{E})\)\(=\displaystyle \left(a-a\cos\theta-a\cos\left(\frac{2\pi}{3}-\theta\right),a\sin\left(\frac{2\pi}{3}-\theta\right)\right)\)
ここで,\(\displaystyle E'\left(a-\frac{\sqrt{3}a}{2},a\right)\),\(\displaystyle E''\left(0,\frac{\sqrt{3}a}{2}\right)\)である.
よって,\(S_{1}\)\(=\displaystyle \int_{0}^{a-\frac{\sqrt{3}a}{2}} (a-y_{E})dx\)
ここで,\(\displaystyle dx=a\sin\theta-a\sin\left(\frac{2\pi}{3}-\theta\right)d\theta\),\(\displaystyle y_{E}=a\sin\left(\frac{2\pi}{3}-\theta\right)\)
\(\displaystyle x:0\rightarrow a-\frac{\sqrt{3}a}{2}\)の時,\(\displaystyle \theta:\frac{\pi}{3}\rightarrow \frac{\pi}{6}\)となる.
よって,\(S_{1}\)\(=\displaystyle \int_{\frac{\pi}{3}}^{\frac{\pi}{6}} \left(a-a\sin\left(\frac{2\pi}{3}-\theta\right)\right)\left(a\sin\theta-a\sin\left(\frac{2\pi}{3}-\theta\right)\right)d\theta\)\(=\displaystyle \int_{\frac{\pi}{3}}^{\frac{\pi}{6}} a^{2}\left(\sin\theta-\sin\left(\frac{2\pi}{3}-\theta\right)+\frac{1}{2}\left(\cos\frac{2\pi}{3}-\cos\left(2\theta-\frac{2\pi}{3}\right)\right)+\frac{1}{2}\left(1-\cos\left(\frac{4\pi}{3}-2\theta\right)\right)\right)d\theta\)\(=\displaystyle a^{2}\left[-\cos\theta-\cos\left(\frac{2\pi}{3}-\theta\right)+\frac{\theta}{4}+\frac{1}{4}\left(\sin\left(2\theta-\frac{4\pi}{3}\right)+\sin\left(\frac{4\pi}{3}-2\theta\right)\right)\right]_{\frac{\pi}{3}}^{\frac{\pi}{6}}\)\(=\displaystyle a^{2}\left(1-\frac{\sqrt{3}}{2}-\frac{\pi}{24}\right)\)
よって,\(S\)\(=a^{2}-4S_{1}\)\(=\displaystyle \left(2\sqrt{3}-3+\frac{\pi}{6}\right)a^{2}\)
※ここで,ルーローの三角形はドリルやロータリーエンジンなど様々なところに適用されている.広範囲を掃除できるということで,掃除機にも適用されています.掃除機の例はこちら(※パナソニックの回し者ではありません.)
正方形の中でルーローの三角形と円で掃ける面積を見てみよう.
円:\(\displaystyle \frac{\pi}{4}a^{2}\)\(\approx 0.7854a^{2}\)
ルーローの三角形:\(\displaystyle \left(2\sqrt{3}-3+\frac{\pi}{6}\right)a^{2}\)\(\approx 0.9877a^{2}\)
と,大きく異なることが分かる.
※パナソニックの回し者ではありません.