上級者
数学Ⅲ:極限
-
ヒント:図形の極限のときにはとにかく関係式を書き出していき,それぞれに当てはめていく.この場合は\(n\)番目の面積を求めるために数列を使い求める.
問題
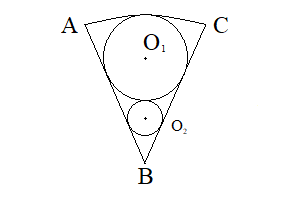
図のように扇形の内部に円が順番に\(B\)に接近しながら接している.円\(O_{n}\)の半径を\(r_{n}\)とし,面積を\(S_{n}\)とする.また,扇形の面積\(T\)とする.このとき,\(\displaystyle \lim_{\angle ABC\rightarrow 0}\frac{\displaystyle \sum_{n=1}^{\infty}S_{n}}{T}\)を求めよ.(オリジナル)
解答
\(\angle ABC=2x\),\(AB=R\)とおく.
まず,\(\sin x=\displaystyle \frac{r_{1}}{R-r_{1}}\) \(\Leftrightarrow\) \(\displaystyle r_{1}=\frac{R\sin x}{1+\sin x}\)
また,\(r_{n}\)と\(r_{n+1}\)について,
\(\sin x=\displaystyle \frac{r_{n}-r_{n+1}}{r_{n}+r_{n+1}}\) \(\Leftrightarrow\) \(\displaystyle r_{n+1}=\frac{1-\sin x}{1+\sin x}r_{n}\)
∴\(r_{n}=\left(\displaystyle \frac{1-\sin x}{1+\sin x}\right)^{n-1}r_{1}\)\(=\displaystyle \left(\frac{1-\sin x}{1+\sin x}\right)^{n}\frac{R\sin x}{1-\sin x}\)
∴\(S_{n}=\displaystyle \pi\left(\frac{R\sin x}{1-\sin x}\right)^{2}\left(\frac{1-\sin x}{1+\sin x}\right)^{2n}\)
∴\(\displaystyle \sum_{n=1}^{\infty}S_{n}\)\(\displaystyle =\pi\left(\frac{R\sin x}{1-\sin x}\right)^{2}\frac{\left(\frac{1-\sin x}{1+\sin x}\right)^{2}}{1-\left(\frac{1-\sin x}{1+\sin x}\right)^{2}}\)\(=\displaystyle \frac{\pi}{4}R^{2}\sin x\)
\(T=\displaystyle \frac{1}{2}R^{2}\times 2x=R^{2}x\)
∴\(\displaystyle \lim_{\angle ABC\rightarrow 0}\frac{\displaystyle \sum_{n=1}^{\infty}S_{n}}{T}\)\(=\displaystyle \lim_{2x\rightarrow 0}\frac{\frac{\pi}{4}R^{2}\sin x}{R^{2}x}\)\(=\displaystyle \lim_{x\rightarrow 0}\frac{\pi}{4}\frac{\sin x}{x}=\frac{\pi}{4}\)
参考入試問題
\(n\)を自然数とする.半径\(\displaystyle \frac{1}{n}\)の円を互いに重なりあわないように半径1の円に外接させる.この時外接する円の最大個数を\(a_{n}\)とする.\(\displaystyle \lim_{n\rightarrow \infty}\frac{a_{n}}{n}\)を求めよ.(1957 東工大)
解答
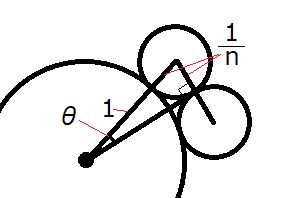
図のように描けるため,\(\sin \theta\)\(=\displaystyle \frac{\frac{1}{n}}{1+\frac{1}{n}}\)\(=\displaystyle \frac{1}{n+1}\cdots\)①
また角度\(\theta\)について,\(2\pi-2\theta<2\theta\times a_{n}\leqq 2\pi\) \(\Leftrightarrow\) \(\displaystyle \frac{\pi}{\theta}-1<a_{n}\leqq \frac{\pi}{\theta}\cdots\)②
①,②より,\(\displaystyle \frac{a_{n}}{n}\)は,\(\displaystyle \frac{\pi-\theta}{\theta}\frac{\sin \theta}{1-\sin \theta}\)\(\displaystyle <\frac{a_{n}}{n}\)\(\displaystyle \leqq \frac{\pi}{\theta}\frac{\sin \theta}{1-\sin \theta}\)
\(n\rightarrow \infty\)の時,\(\theta\rightarrow 0\)より,不等式の右辺と左辺は,\(\pi\)に収束する.よって,\(\displaystyle \lim_{n\rightarrow \infty}\frac{a_{n}}{n}=\pi\)