MATH

ヒント：\(n\)回目の確率が\(n-1\)回目の確率と関係するとき，漸化式を立てることを考えよう．

1,2,3のカードが入った箱がある．\(n\)回カードを引いたときに，\(1,\cdots,n\)回目のカードの和が2の倍数になる確率を求めよ．（オリジナル）

解説

\(n+1\)回目までの和が2の倍数の時の確率を\(p_{n+1}\)と表す時，

\(n\)回目までの和が2の倍数の時の確率は\(p_{n}\)となる．

一方で，\(n\)回目までの和が2の倍数でない確率は\(1-p_{n}\)である．

また，\(n\)回目までの和が2の倍数の時，\(n+1\)回目が2の倍数になるには2のカードを引く必要がある．その確率は\(\displaystyle \frac{1}{3}\)である．

一方で，\(n\)回目までの和が2の倍数でない時，\(n\)回目が2の倍数になるには，1,3のカードを引く必要がある．その確率は\(\displaystyle \frac{2}{3}\)である．

よって，\(\displaystyle p_{n+1}=\frac{1}{3}p_{n}+\frac{2}{3}(1-p_{n})\) \(\Leftrightarrow\) \(\displaystyle p_{n+1}-\frac{1}{2}=-\frac{1}{3}\left(p_{n}-\frac{1}{2}\right)\)

\(p_{1}=\displaystyle \frac{1}{3}\)より，\(p_{n}=\displaystyle \frac{1}{2}-\frac{1}{6}\left(-\frac{1}{3}\right)^{n-1}\)

\(n\)回目と\(n+1\)回目の対応

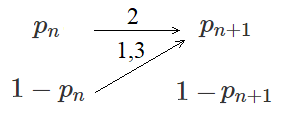
直線上に赤と白の旗を持った何人かが，番号\(0,1,2,…\)をつけて並んでいる．番号0の人は，赤と白を等しい確率で無作為に上げるものとし，他の番号\(j\)の人は，番号\(j−1\)の人のあげた旗の色を見て，確率\(p\)で同じ色，確率\(1−p\)で異なる色の旗をあげるものとする．このとき，番号0の人と番号\(n\)の人が同じ色の旗をあげる確率\(P_{n}\)を求めよ．(1983 東大)

考え方　0と\(n\)が同じ確率が\(p_{n}\)とおかれているので，0と\(n+1\)が同じ確率は\(p_{n+1}\)となる．そして，\(n\rightarrow n+1\)になるときにはどうなるのかを考えればよい．確率漸化式と呼ばれるもので，ある程度のレベルの大学で出題されることがある．

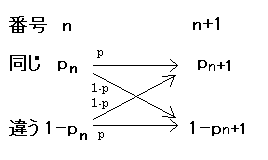
図から\(p_{n+1}=p_{n}\times p+(1-p_{n})(1-p)\)…①

\(1-p_{n+1}=p_{n}\times(1-p)+(1-p_{n})\times p\)…②

（①と②は実は同じなので，①だけを考える．）

① ⇔ \(p_{n+1}=(2p-1)p_{n}+1-p\)…③

ここで数列の等比数列型に変形すると

\(p_{n+1}+a=(2p-1)(p_{n}+a)\Leftrightarrow p_{n+1}=(2p-1)p_{n}+2(p-1)a\)…④

③，④の係数を比較すると，\(2(p-1)a=1-p\displaystyle \Leftrightarrow a=-\frac{1}{2}\)

∴\(p_{n+1}-\displaystyle \frac{1}{2}=(2p-1)\left(p_{n}-\frac{1}{2}\right)\Leftrightarrow p_{n}-\frac{1}{2}=(2p-1)^{n}\left(p_{0}-\frac{1}{2}\right)\)

ここで，\(p_{0}\)において番号0=番号0より\(p_{0}=1\)

∴\(p_{n}=\displaystyle \frac{1}{2}(2p-1)^{n}+\frac{1}{2}\)