上級者
数学Ⅰ:二次関数
-
ヒント:1.二次関数と直線の問題については,交点を文字で置いてから範囲を考慮しながらその文字を消していくという方法を取ると,スムーズに問題が解ける.2.最大値について書いてありますが,この場合は範囲を求めることにします.実際範囲を求めればおのずと最大値がわかるという考えです.
問題
今,\(y=a^{3}x^{2}\)となるグラフに上から\(\displaystyle \frac{1}{a}\)の棒を落とす.このときに棒と放物線が囲む面積の最大値が\(a\)に無関係であることを求めよ.(オリジナル)
解説
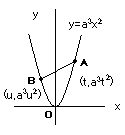
図のように点を取る(\(t>u\)としてもよい).ここで面積を\(S\)とおくと,
\(S=\displaystyle \int_{u}^{t}\{(ABの直線)-a^{3}x^{2}\displaystyle \}\)\(=\displaystyle -\frac{1}{6}(-a^{3})(t-u)^{3}\)\(=\displaystyle \frac{a^{3}}{6}(t-u)^{3}\)
一方,三平方の定理より,\(\left(\displaystyle \frac{1}{a}\right)^{2}=(t-u)^{2}+a^{6}(t^{2}-u^{2})^{2}\)
ここで,\(t−u=s(s>0)\)とおくと,\(S=\displaystyle \frac{a^{3}}{6}s^{3}\)
\(\left(\displaystyle \frac{1}{a}\right)^{2}=s^{2}+a^{6}s^{2}(2t-s)^{2}\)
ここで\(S\)が最大となるときの\(s\)を求める.ここでは\(s\)の範囲を求めることにする.
(∵\(s\)の範囲を出せば,おのずと最大値はわかる)
\(\left(\displaystyle \frac{1}{a}\right)^{2}=s^{2}+a^{6}s^{2}(2t-s)^{2}\)\(\Leftrightarrow\) \(4a^{8}s^{2}t^{2}-4a^{8}s^{3}t+a^{8}s^{4}+a^{2}s^{2}-1=0\)
まずここが難しいのだが,これを\(s\)の方程式と見るのではなくて,\(t\)の方程式と見る.
というのは見たとおり,\(s=\)の式に直すのは困難である.
ここでの考えは\(t\)の方程式と見ることで,\(t\)の式から\(s\)のとりうる範囲を求めるという事を行う.
(ここでの\(t\)の範囲は実数解だが,範囲が限られているときもあるから注意.)
ここで\(t\)は実数解より,判別式から,(←判別式は実数解だからという口実によく使われる.)
\((-2a^{8}s^{3})^{2}-4a^{8}s^{2}(a^{8}s^{4}+a^{2}s^{2}-1)\geqq 0\) \(\Leftrightarrow\) \(4a^{8}s^{2}(1-a^{2}s^{2})\geqq 0\)
∴\(1-a^{2}s^{2}\geqq 0\) \(\Leftrightarrow\) \(\displaystyle 0<s\leqq \frac{1}{a}\)
よって\(S\)の最大値は\(s=\displaystyle \frac{1}{a}\)で,\(S=\displaystyle \frac{1}{6}\)となり,\(a\)に無関係である.
※なお,(\(\displaystyle t=\frac{1}{2a}\),\(\displaystyle u=-\frac{1}{2a}\))となる.