上級者
関数
-
ヒント:1.最大値,最小値を求める=範囲を求める.2.与えられた式\(=k\)と置く.3.求めたい範囲の関数を別の関数で置き,範囲を求める.
問題
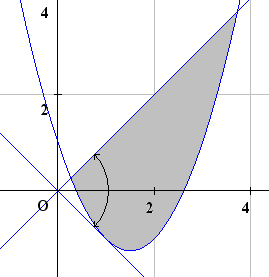
\(x,y\)が2つの不等式\(x \geqq y\cdots\)①,\(y\geqq x^{2}-3x+1\cdots\)②を満たすとき,
\(\displaystyle \frac{x^{2}}{3x^{2}-4xy+2y^{2}}\)のとりうる値の最大値,最小値を求めよ.(オリジナル)
解答
まず,\(x=0\)のとき,①\(\Leftrightarrow\) \(y\leqq 0\),②\(\Leftrightarrow\) \(y\geqq 1\)となるので,不適となる.よって\(\displaystyle \frac{x^{2}}{3x^{2}-4xy+2y^{2}}=\frac{1}{k}\)とおける.(\(k\)は実数の範囲)
変形させて\((3-k)x^{2}-4xy+2y^{2}=0\) \(\Leftrightarrow\) \(\displaystyle 2\left(\frac{y}{x}\right)^{2}-4\left(\frac{y}{x}\right)+3-k=0\)で,\(t=\displaystyle \frac{y}{x}\)とおくと,\(2t^{2}-4t+3-k=0\) \(\Leftrightarrow\) \(2(t-1)^{2}+1-k=0\cdots\)③
ここで,\(y=tx\)で①,②を満たす\(t\)の範囲は\(−1\leqq t\leqq1\cdots\)④となる.
\(f(t)=2(t-1)^{2}+1-k\),\(f(1)=1−k\),\(f(−1)=9−k\)
③④より,\(1−k\leqq 0 \leqq 9−k\)\(\Leftrightarrow\) \(1\leqq k\leqq 9\)
よって最大値は9,最小値は1となる.