上級者
二次関数
-
文系の範囲で解ける問題です.計算を適切に行い,文字を置いたときの範囲を忘れないでください.
問題
1辺の長さが\(1,1,\sqrt{2}\)の直角二等辺三角形を底面とし高さが1の三角柱を考える.この三角柱を平面で切り,その断面が3辺とも三角柱の側面上にある正三角形であるようにする.そのような正三角形の面積がとりうるような値の範囲を求めよ.(類 東工大)
解答
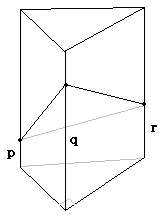
一般的に図のように長さを決めることができる.正三角形であることから\((q-p)^{2}+1^{2}=(q-r)^{2}+1^{2}=(r-p)^{2}+\sqrt{2}^{2}\)
これから\(p^{2}-2pq=r^2-2qr\)…①,\(q^{2}-2pq=r^2-2pr+1\)…②
また,面積\(S=\displaystyle \frac{\sqrt{3}}{4}((r-p)^{2}+2)\)…③
条件は\(0\leqq p,q,r\leqq 2\)…④
ここで,正三角形の条件から\(p-r\)が別の2つと異なるため,まずは\(p-r=t\)…④と置く.
面積\(S\)は\(S=\displaystyle \frac{\sqrt{3}}{4}(t^{2}+2)\)…③
①,④より\(r\)を消去すると,\(t(t-2(p-q))=0\)
(A) \(t=0\)の時,\(p=r\)
③より,\(q=p+1=r+1\)で条件④が成立する.
これより,面積\(S=\displaystyle \frac{\sqrt{3}}{2}\)
(B) \(t=2(p-q)\)の時,③に代入すると,\(3(q-p)^2+1=0\)なので,成立する解はない.
よって,求める面積は\(\displaystyle \frac{\sqrt{3}}{2}\)
参考入試問題
1辺の長さが1の正三角形を底面とし高さが2の三角柱を考える.この三角柱を平面で切り,その断面が3辺とも三角柱の側面上にある直角三角形であるようにする.そのような直角三角形の面積がとりうるような値の範囲を求めよ.(2000 東工大)
解説
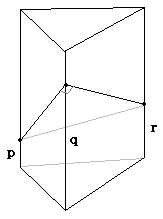
一般的に図のように長さを決めることができる.直角三角形であることから\((q-p)^{2}+1^{2}+(q-r)^{2}+1^{2}=(r-p)^{2}+1^{2}\)
これから\(2q^{2}-2qp-2qr+2rp+1=0\)…①
また,面積\(S=\displaystyle \frac{1}{2}\sqrt{(q-p)^{2}+1^{2}}\sqrt{(q-r)^{2}+1^{2}}\)…②
条件は\(0\leqq p,q,r\leqq 2\)
つまり,二つしか式がないのに変数が3つあるので非常に難しくなります.
そこでよく考えてみると直角三角形を決めるときはp=一定と考えてもよく,また,面積をとりうる範囲を考えるのに最大をとる場合を考えるとp=0の時であると考えられる.
このように設定によって変数を減らすことができる.
よって次のような式となる.
\(2q^{2}-2qr+1=0\)…①
\(S=\displaystyle \frac{1}{2}\sqrt{(q^{2}+1)\{(q-r)^{2}+1\}}\)…②
①から\(q\neq 0\)であるので,\(r=\displaystyle \frac{2q^{2}+1}{2q}\)
これを②に代入して
\(S=\displaystyle \frac{1}{2}\sqrt{(q^{2}+1)(\frac{1}{4q^{2}}+1)}\)\(=\frac{1}{2}\sqrt{q^{2}+\frac{5}{4}+\frac{1}{4q^{2}}}\)
\(0\leqq r\leqq 2\)から\(0\displaystyle \leqq\frac{2q^{2}+1}{2q}\leqq 2\)これより,\(\displaystyle \frac{2-\sqrt{2}}{2}\leqq q\leqq\frac{2+\sqrt{2}}{2}\)
\(f(q)=q^{2}+\displaystyle \frac{5}{4}+\frac{1}{4q^{2}}\)\(=(q+\frac{1}{2q})^{2}+\frac{1}{4}\)
\(f'(q)=\displaystyle \frac{4q^{4}-1}{2q^{3}}\)から次のような増減表を得る.
\begin{array}{c|c|c|c|c}
q & \frac{2-\sqrt{2}}{2} &\cdots & \frac{1}{\sqrt{2}} & \cdots & \frac{2+\sqrt{2}}{2} \\ \hline
f'(q)& &- & 0 & + & \\ \hline
f(q) &\frac{17}{4} &\searrow& \frac{9}{4} &\nearrow& \frac{17}{4} \\ \hline
\end{array}
よって\(S\)の範囲は\(\displaystyle \frac{3}{4}\leqq S\leqq\frac{\sqrt{17}}{4}\)となる.
※\(r\)について解くとさらに簡単に解ける.
\(r=\displaystyle \frac{2q^{2}+1}{2q}\)\(=\displaystyle q+\frac{1}{2q}\geqq 2\sqrt{q\cdot\frac{1}{2q}}=\sqrt{2}\) (等号成立は\(q=\displaystyle \frac{1}{\sqrt{2}}\))
よって\(\sqrt{2}\leqq r\leqq 2\)
また,\(S=\displaystyle \frac{1}{2}\sqrt{(q^{2}+1)(\frac{1}{4q^{2}}+1)}\)\(=\displaystyle \frac{1}{2}\sqrt{q^{2}+\frac{5}{4}+\frac{1}{4q^{2}}}=\frac{1}{2}\sqrt{(q+\frac{1}{2q})^{2}+\frac{1}{4}}\)\(=\displaystyle \frac{1}{2}\sqrt{r^{2}+\frac{1}{4}}\)
よって\(S\)の範囲は\(\displaystyle \frac{3}{4}\leqq S\leqq\frac{\sqrt{17}}{4}\)となる.