中級者
数学Ⅰ:二次関数
-
ヒント:絶対値についてしっかりと場合分けを行おう.グラフを描くとより分かりやすくなる.
問題
\(|x^{2}-2x-4|<2|x|+1\)の不等式を解け.
解答
不等式の場合分けで解く.
\(x^{2}-2x-4<0\) \(\Leftrightarrow\) \(1-\sqrt{5}<x<1+\sqrt{5}\)を基準とする.
①\(x^{2}-2x-4<0,~x<0\)の場合\((1-\sqrt{5}<x<0)\)
\(-x^{2}+2x+4<-2x+1\) \(\Leftrightarrow\) \(x^{2}-4x-3>0\) \(\Leftrightarrow\) \(x<2-\sqrt{7},~x>2+\sqrt{7}\)
\(1-\sqrt{5}<2-\sqrt{7}\)なので,\(1-\sqrt{5}<x<2-\sqrt{7}\)
②\(x^{2}-2x-4<0,~x\geqq 0\)の場合\((0\leqq x<1+\sqrt{5})\)
\(-x^{2}+2x+4<2x+1\) \(\Leftrightarrow\) \(x^{2}-3>0\) \(\Leftrightarrow\) \(x<-\sqrt{3},~x>\sqrt{3}\)
\(\sqrt{3}<1+\sqrt{5}\)なので,\(\sqrt{3}<x<1+\sqrt{5}\)
③\(x^{2}-2x-4\geqq 0,~x<0\)の場合\((1-\sqrt{5}\geqq x)\)
\(x^{2}-2x-4<-2x+1\) \(\Leftrightarrow\) \(x^{2}<5\) \(\Leftrightarrow\) \(-\sqrt{5}<x\sqrt{5}\)
\(-\sqrt{5}<1-\sqrt{5}\)なので,\(-\sqrt{5}<x\leqq 1-\sqrt{5}\)
④\(x^{2}-2x-4\geqq 0,~x\geqq 0\)の場合\((x\geqq 1+\sqrt{5})\)
\(x^{2}-2x-4<2x+1\) \(\Leftrightarrow\) \(x^{2}-4x-5<0\) \(\Leftrightarrow\) \(-1<x<5\)
よって,\(1+\sqrt{5}\leqq x<5\)
以上から
\(-\sqrt{5}<x<2-\sqrt{7},~\sqrt{3}<x<5\)
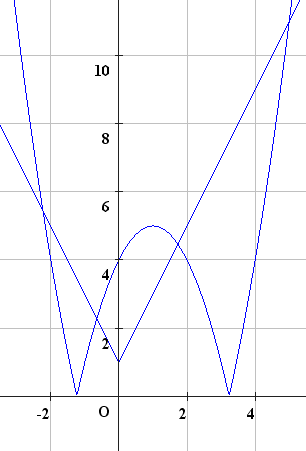
別解
グラフの交点を求めて,不等式を満たすような範囲を求める.
参考入試問題
関数\(f(x)=x^{2}-4|x|+k\)の最小値を\(m(k)\),最大値を\(M(k)\)とする.
(1)\(m(k)=2\)のとき,定数\(k\)の値を求めよ.
(2)\(−1≦x≦5\)のとき,\(m(k),M(k)\)を\(k\)で表せ.
(3)\(f(x)=0\)の解が4つになるような\(k\)の値の範囲を求めよ.
(4)関数\(y=f(x)\)のグラフを直線\(y=k\)に関して対称移動するとき,その関数の最大値を求めよ.(00滋賀医大)
解答
グラフを書けば,ほとんど分かる.
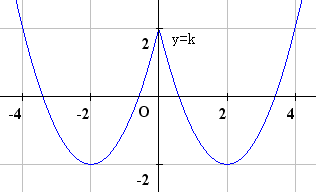
(1)すべての\(x\)の範囲では最小値\(m(k)=k−4\)となる.
よって\(k=6\)
(2)最小値は\(x=2\)で,\(m(k)=k−4\) 最大値は\(x=5\)で,\(M(k)=k+5\)
(3)\(f(x)=0\)の解が4つ ⇔ グラフで\(x\)軸との交点が4つ
よって\(k−4<0<k\) ⇔ \(0<k<4\)
(4)\(y=k\)に関して対称移動すると,関数は\(y=-x^{2}+4|x|+k\)となり,最大値は\(x=\pm 2\)で\(k+4\)
チェック
\(y=f(x)\)を\(x=a\)で対称移動すると,\(y=f(−x+2a)\)となる.