中級者
数学B:ベクトル
-
ヒント:図形の長さ,角度,座標を使い,ベクトルの直線状に点がある条件を使うことがよくあるが,基本的には,図形を解く場合の補助と考えてよい.使いこなせるようになれば,計算処理が速くなる.
問題
\(P\)を\(△ABC\)の内部の点とし,\(△BPC\),\(△CPA\),\(△APB\)の面積の比が\(1:1:1\)になるとき,点\(P\)は重心であることを示せ.(重心の性質)
解答
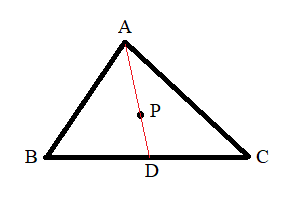
\(AP\)を延長して\(BC\)と交わる点を\(D\)とすると,\(△ABC:△BPC=3:1\)より,\(AD:AP=3:2\)
∴\(\displaystyle \overrightarrow{AP}=\frac{2}{3}\overrightarrow{AD}\)
また,\(△ABP:△ACP=1:1\)より,\(BD:CD=1:1\)
これより,\(D\)は\(A\)と\(B\)の中点となる.
ここで,重心の定義は中線の交点\(G\)である.また,重心\(G\)は中線を2:1で分割する.つまり,\(\displaystyle \overrightarrow{AG}=\frac{2}{3}\overrightarrow{AD}\)
参考入試問題
\(P\)を\(△ABC\)の内部の点とし,\(△BPC\),\(△CPA\),\(△APB\)の面積の比が\(1:2:3\)になるとき
(1) \(\overrightarrow{AP}\)を\(\overrightarrow{AB}\),\(\overrightarrow{AC}\)で表せ.
(2) \(a \overrightarrow{PA}+b \overrightarrow{PB}+c \overrightarrow{PC}=\overrightarrow{0}\)とするとき,\(a:b:c\)を求めよ.ただし,\(abc\neq 0\) (1999 琉球大)
解答
\(AP\)を延長して\(BC\)と交わる点を\(D\)とすると,\(△ABC:△BPC=6:1\)より,\(AD:AP=6:5\)
∴\(\displaystyle \overrightarrow{AP}=\frac{5}{6}\overrightarrow{AD}\cdots\)①
また,\(△ABP:△ACP=3:2\)より,\(BD:CD=3:2\)
∴\(\displaystyle \overrightarrow{AD}=\frac{2\overrightarrow{AB}+3\overrightarrow{AC}}{5}\cdots\)②
①,②より,\(\displaystyle \overrightarrow{AP}=\frac{2\overrightarrow{AB}+3\overrightarrow{AC}}{6}\)
(2) (1)より,\(\displaystyle 6\overrightarrow{AP}=2\overrightarrow{AB}+3\overrightarrow{AC}\) \(\Leftrightarrow\) \(2(\overrightarrow{PB}-\overrightarrow{PA})\)\(+3(\overrightarrow{PC}-\overrightarrow{PA})\)\(+6\overrightarrow{PA}=\overrightarrow{0}\)
∴\(\overrightarrow{PA}+2\overrightarrow{PB}+3\overrightarrow{PC}=\overrightarrow{0}\)
よって,\(a=1\),\(b=2\),\(c=3\)