小休止
コラム:解と係数の関係
¶解と係数の関係
解と係数の関係は教科書ではあまり大きく扱っていないですが,入試問題では非常に多く使う場面があります.ここで使い方を覚えましょう.
使い方としては計算をより簡単に行うために使い,楽に問題を解けるようにすることです.これは具体的に問題を見ていくといいでしょう.
問題1
(2001 一橋大)
放物線\(y=x^{2}\)上に,直線\(y=ax+1\)に関して対称な位置にある異なる2点\(P,Q\)が存在するような\(a\)の値の範囲を求めよ.
解説
こういう問題は非常に出やすいので,覚えておくこと.重要なのは解答にある①,②のことである.
解答
点\(P,Q\)は放物線上にあるので,\(P(p,p^{2})\), \(Q(q,q^{2})\)とおける.\((p\neq q)\)
ここで条件は2つある.
①直線\(PQ\)が直線\(y=ax+1\)と垂直に交わる.
②点\(P,Q\)の中点が直線\(y=ax+1\)の上にある.
①について
直線\(PQ\)の傾きは\(\displaystyle \frac{p^{2}-q^{2}}{p-q}=p+q\)である.よって\((p+q)a=-1\)…①
②について
点\(P,Q\)の中点は\(\left(\displaystyle \frac{p+q}{2},\frac{p^{2}+q^{2}}{2}\right)\)である.よって\(\displaystyle \frac{p^{2}+q^{2}}{2}=a\frac{p+q}{2}+1\)…②
次に考えることは\(a\)の存在範囲を考えるのに,文字を減らすことである.
文字を減らす方法は2つある.
1つ目
①,②から\(q\)を消去すると,\(2a^{2}p^{2}+2ap+1-a^{2}=0\) \((a\neq 0)\)
ここで,\(p\)の範囲を考えると,実数全体を動く.よって,上の式が成り立つ条件は判別式\(D≧0\)
\(D/4=a^{2}-2a^{2}(1-a^{2})=a^{2}(2a^{2}-1)\geqq 0\)
また,\(a=0\)の時は成り立たない.
ここで,\(p \neq q\)が条件であるので,\(p=q\)の時,\(a\)の値は\(a=\displaystyle \pm\frac{1}{\sqrt{2}}\)
これより,\(a>\displaystyle \frac{1}{\sqrt{2}}\),\(\displaystyle a<-\frac{1}{\sqrt{2}}\)
2つ目
ここで,①,②を見ると,対称式となっている.
☆対称式とは
文字を入れ替えても式自体が変わらない式のこと.ここでは\(p,q\)を入れ変えても式は変わらない.
2つの文字の対称式の場合,式を\(p+q,pq\)の形で表せる.→この形は解と係数の関係が使える!
よって①から\(a \neq 0\)のとき,\(p+q=-\displaystyle \frac{1}{a}\)…③
②から\((p+q)^{2}-2pq=a(p+q)+2\) \(\Leftrightarrow\) \(\displaystyle pq=\frac{1-a^{2}}{2a^{2}}\)…④
これより,解と係数の関係から\(p,q\)は\(t^{2}+\displaystyle \frac{1}{a}t+\frac{1-a^{2}}{2a^{2}}=0\)の異なる2つの実数解となる.(この式は実は1つ目でやった式と同じである.しかし,判別式\(D>0\)である.)
また\(a=0\)の時は成り立たない.答えは\(a>\displaystyle \frac{1}{\sqrt{2}}\),\(\displaystyle a<-\frac{1}{\sqrt{2}}\)
問題2
(2000 関西大)
座標平面上の点\((p,q)\)は\(x^{2}+y^{2}\leqq 8\),\(y\geqq 0\)であらわされる領域を動く.点\((p+q,pq)\)の動く範囲を図示せよ.
解説
点の軌跡を考えるときは点\((x,y)\)としないと動きが分からないので,ここで\(x=p+q\),\(y=pq\)とおく.ここで上でもやったが,\(p+q\),\(pq\)の形は解と係数の関係が使えるので積極的に使っていこう.
解答
点\((p,q)\)が\(x^{2}+y^{2}\leqq 8\),\(y\geqq 0\)であらわされる領域を動くので,\(p^{2}+q^{2}\leqq 8\),\(q\geqq 0\)…①となる.また,\(x=p+q\),\(y=pq\)とおく.すると,①を\(x,y\)の式に変形すると,
\(x^{2}-2y\leqq 8\),\(q\leqq 0\)…②
また,解と係数の関係より,\(p,q\)は二次方程式\(t^{2}-xt+y=0\)の解である.ここで,\(q \leqq 0\)なので,二次方程式の解の一つは0以上の解となる.
ここで,式を整理する.\(p^{2}+q^{2}\leqq 8\),\(q\geqq 0\),\(x=p+q\),\(y=pq\) \(\Leftrightarrow\) \(x^{2}-2y\leqq 8\),\(t^{2}-xt+y=0\)の解の一つは0以上の解となる.
\(t^{2}-xt+y=0\)について条件は\(f(t)=t^{2}-xt+y\)\(=\displaystyle \left(t-\frac{x}{2}\right)^{2}+y-\frac{x^{2}}{4}\)とおく.
(1)\(t≧0\)で1つか2つ解を持つとき
\(f(0)≦0\)が条件となる.よって\(y≦0\)
(2)\(t≧0\)で2つ解を持つとき
\(\displaystyle \frac{x}{2}\geqq 0\),\(\displaystyle y-\frac{x^{2}}{4}\leqq 0\),\(f(0)\geqq 0\)
これより,\(x\displaystyle \geqq 0\),\(\displaystyle y\leqq\frac{x^{2}}{4}\),\(y\geqq 0\)
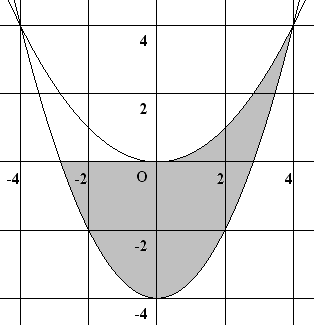
以上から,(\(y≦0\)または\(x\displaystyle \geqq 0\),\(\displaystyle y\leqq\frac{x^{2}}{4}\),\(y\geqq 0\))かつ\(x^{2}-2y\leqq 8\)を満たすような領域が答えとなる.
日々問題でも扱ってます.こちら