上級者
三角関数・整題
問題(オリジナル)
直角三角形の三辺は三平方の定理より,\(a^2+b^2=c^2\)が成立するが,三辺が整数かつ互いに素である場合,ある正の整数\(m,n\)\((m>n)\)を用いて,\((m^{2}-n^{2})^{2}\)\(+(2mn)^{2}\)=\((m^{2}+n^{2})^{2}\)が成立する.この性質を使い,次の問題を解け.
(1)\(m=3\),\(n=2\)の時,三角形の最小となる角度\(\theta^{\circ}\)とする.
この時,図の三角形ABDと扇形ABDと三角形AEFの面積の大きさを比較することで,\(\theta^{\circ}\)の大きさを整数部分まで求めよ.
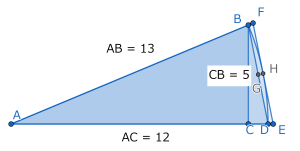
(2)三辺が整数かつ互いに素である場合,直角三角形の斜辺ともう一つの辺の差が1の時,残りの一辺は1以外の奇数になることを示せ.
(3)三辺が整数かつ互いに素である場合,辺の最小の長さを100以下とした時,最小となる角度\(\theta^{\circ}\)について,小数点第三位まで求めよ.
解答はこちら