上級者
三角関数・整数
-
ヒント:(1),(2)は(3)の誘導問題です.(1),(2)は頑張って計算しましょう.
問題
直角三角形の三辺は三平方の定理より,\(a^2+b^2=c^2\)が成立するが,三辺が整数かつ互いに素である場合,ある正の整数\(m,n\)\((m>n)\)を用いて,\((m^{2}-n^{2})^{2}\)\(+(2mn)^{2}\)=\((m^{2}+n^{2})^{2}\)が成立する.この性質を使い,次の問題を解け.
※上記の関係を求める方法は,こちらの参考入試問題を参考にして下さい.
(1)\(m=3\),\(n=2\)の時,三角形の最小となる角度\(\theta^{\circ}\)とする.
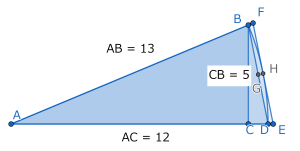
この時,図の三角形ABDと扇形ABDと三角形AEFの面積の大きさを比較することで,\(\theta^{\circ}\)の大きさを整数部分まで求めよ.
(2)三辺が整数かつ互いに素である場合,直角三角形の斜辺ともう一つの辺の差が1の時,残りの一辺は1以外の奇数になることを示せ.
(3)三辺が整数かつ互いに素である場合,辺の最小の長さを100以下とした時,最小となる角度\(\theta^{\circ}\)について,小数点第三位まで求めよ.
解答
(1)
三角形ABDの面積=\(\displaystyle \frac{1}{2}\times 13\times 5\)
扇型ABDの面積=\(\displaystyle \frac{1}{2}\times 13\times 13\frac{\pi}{180}\theta\)
三角形AEFの面積=三角形ABDの面積\(\displaystyle \times \frac{AH}{AG}\)
ここで,\(AH=AB=13\),\(AG=\sqrt{AB^{2}-BG^{2}}\),\(\displaystyle BG=\frac{BD}{2}=\frac{\sqrt{BC^{2}+CD^{2}}}{2}\)
面積の大小より,三角形ABDの面積<扇型ABDの面積<三角形AEFの面積
各値を代入すると,\(\displaystyle \frac{1}{2}\times 13\times 5\)\(<\displaystyle \frac{1}{2}\times 13\times 13\frac{\pi}{180}\theta\)\(<\displaystyle \frac{1}{2}\times 13\times \sqrt{26}\)\(\Leftrightarrow\)\(\displaystyle \frac{5}{13}\frac{180}{\pi}<\theta<\frac{\sqrt{26}}{13}\frac{180}{\pi}\)
ここで,\(3.14<\pi<3.142\),\(5<\sqrt{26}<5.1\)なので,
\(\displaystyle \frac{5}{13}\frac{180}{\pi}\)\(>\displaystyle \frac{5}{13}\frac{180}{3.142}\)\(>22.03\),\(\displaystyle \frac{\sqrt{26}}{13}\frac{180}{\pi}\)\(<\displaystyle \frac{5.1}{13}\frac{180}{3.14}\)\(<22.49\)
よって,整数部分は22
(2)
\(a=m^{2}-n^{2}\),\(b=2mn\),\(c=m^{2}+n^{2}\)と置く.
\(a,b,c\)は互いに素で,\(b\)は偶数なので,\(a,c\)は奇数となる.
また,\(a<c\),\(b<c\)が成り立つ.
よって,直角三角形の斜辺ともう一つの辺の差が1の場合は,\(c-b=1\)の場合のみである.
よって,\(m^{2}+n^{2}-2mn=1\)\(\Leftrightarrow\)\((m-n)^{2}=1\)
ここで\(a>0\)より,\(m>n\)
よって,\(m-n=1\)
ここで,\(a=m+n=2n+1\)
\(n\geqq 1\)なので,\(a\)は3以上の奇数であり,残りの一辺は1以外の奇数が全て求められることが示された.
(3)
最小の辺の長さに対する角度の指標として,例えば(1)の場合,\(\displaystyle \cos\theta=\frac{AC}{AB}=\frac{12}{13}\)であり,\(\displaystyle \cos\theta\)の値が1に近いほど,最小の辺の長さに対する角度が最も小さくなると言える.つまり,\(AB-AC\)の値が小さく,かつ\(AB\)の値が大きいほど最小の辺の長さに対する角度が最も小さくなる.
よって,最小の辺の長さを100から小さくしていき,その時の\(\displaystyle \cos\theta\)を確認すればよい.
(i)最小の辺の長さが100の場合
\(b\)が偶数なので,\(b=2mn=100\)
よって,\(mn=50\)
この時,\(a=m^{2}-n^{2}\),\(c=m^{2}+n^{2}\)の差が小さくなるには,\(n=1,m=50\)であればよい.
つまり,\(a=m^{2}-n^{2}=2499\),\(c=m^{2}+n^{2}=2501\)である.
よって,\(\displaystyle \cos\theta=\frac{2499}{2501}\)
(ii)最小の辺の長さが99の場合
他の辺の差が最も小さい1が第一候補となり,これは(2)より,\(n=44,m=45\)であることから,
\(a=99,b=4900,c=4901\)である.
よって,\(\displaystyle \cos\theta=\frac{4900}{4901}\)
\(\displaystyle \cos\theta=\frac{4900}{4901}\)\(>\displaystyle \frac{2499}{2501}\)
より,\(a=99,b=4900,c=4901\)の場合が,最も角度が小さくなる.
この時,
三角形ABDの面積=\(\displaystyle \frac{1}{2}ac\)
扇型ABDの面積=\(\displaystyle \frac{1}{2}c^{2}\frac{\pi}{180}\theta\)
三角形AEFの面積=\(\displaystyle \frac{1}{2}ac\frac{c}{AG}\)
ここで,\(\displaystyle AG^{2}=c^{2}-\left(\frac{\sqrt{a^{2}+(c-b)^{2}}}{2}\right)^{2}\)
また,\(c=m^{2}+n^{2}\)\(=(n+1)^{2}+n^{2}\)\(=2n^2+2n+1\)\(=\displaystyle \frac{(2n+1)^{2}+1}{2}\)\(=\displaystyle \frac{a^{2}+1}{2}\)
よって,\(\displaystyle AG^{2}=\left(\frac{a^{2}+1}{2}\right)^{2}-\left(\frac{\sqrt{a^{2}+1}}{2}\right)^{2}\)\(=\displaystyle \frac{a^{2}(a^{2}+1)}{4}\)
よって,
\(\displaystyle \frac{1}{2}ac\)\(<\displaystyle \frac{1}{2}c^{2}\frac{\pi}{180}\theta\)\(<\displaystyle \frac{1}{2}ac^{2}\frac{2}{a\sqrt{a^{2}+1}}\)\(\Leftrightarrow\)\(\displaystyle \frac{a}{a^{2}+1}\frac{360}{\pi}\)\(<\theta\)\(<\displaystyle \frac{1}{\sqrt{a^{2}+1}}\frac{360}{\pi}\)
ここで,\(a=99\),\(3.141<\pi<3.142\)より,
\(\displaystyle \frac{a}{a^{2}+1}\frac{360}{\pi}\)\(>\displaystyle \frac{99}{99^{2}+1}\frac{360}{3.142}\)\(>1.1572\)
\(\displaystyle \frac{1}{\sqrt{a^{2}+1}}\frac{360}{\pi}\)\(<\displaystyle \frac{1}{a}\frac{360}{\pi}\)\(<\displaystyle \frac{1}{99}\frac{360}{3.141}\)\(<1.1578\)
よって,1.157が答えになる.
※(3)の途中結果から辺の最小の長さをX以下と,一般化した場合,
(A)\(X\)が奇数の場合,
\(\displaystyle \frac{X}{X^{2}+1}\frac{360}{\pi}\)\(<\theta\)\(<\displaystyle \frac{1}{\sqrt{X^{2}+1}}\frac{360}{\pi}\)
(B)\(X\)が偶数の場合,
\(\displaystyle \frac{(X-1)}{(X-1)^{2}+1}\frac{360}{\pi}\)\(<\theta\)\(<\displaystyle \frac{1}{\sqrt{(X-1)^{2}+1}}\frac{360}{\pi}\)
となる.
〇参考入試問題:(1)は以下の問題と同じです.
3辺の長さが5,12,13である三角形において,長さが12,13である2辺によってはさまれる角の大きさを\(\theta\)とする。このとき \(n^{\circ}<\theta<(n+1)^{\circ}\)となる整数\(n\)は\(\square\)である.(2007 早稲田大)