MATH

積分法

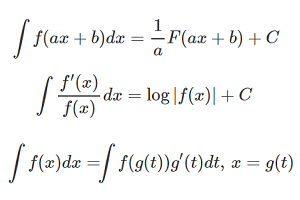
問題：\(n\)を正の整数とするとき，(i)\(a_{n}\)\(=\int_{0}^{n\pi}e^{-x}\sin x dx\)を求めよ．(ii)\(\lim_{n\rightarrow\infty}a_{n}\)を求めよ．

積分法

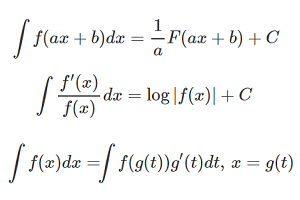
問題：\(\int_{0}^{1}\frac{x^4(1-x)^4}{2}dx\)\(<\int_{0}^{1}\frac{x^4(1-x)^4}{1+x^2}dx\)\(<\int_{0}^{1}x^4(1-x)^4dx\)の式を用い，\(\pi\)を小数点第2位まで求めよ．

積分法

問題：\(y=\displaystyle \frac{1}{\sqrt{x^{2}+1}}\)となるグラフに対し，\(0\leqq x\leqq\sqrt{3}\)の範囲で，\(y\)軸を軸として回転させたときにできる立体の体積を求めよ．