MATH

数列

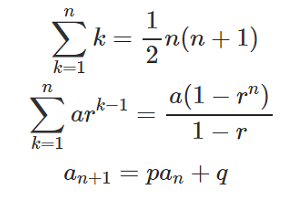
問題：(1) 2以上の整数\(n\)に対し，\(\displaystyle \frac{1}{1\cdot2}+\frac{1}{2\cdot3}+\cdots+\frac{1}{n(n+1)}\)を求めよ． (2) 任意の正の整数\(n\)に対し，\(\displaystyle \frac{1}{1^2}+\frac{1}{2^2}+\cdots+\frac{1}{n^2}\)\(<2\)が成り立つことを示せ．

数列

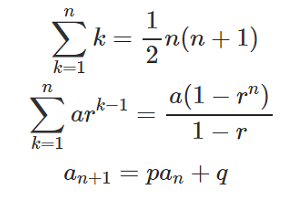
問題：ここに3つの異なる数があるとする．それを小さい順に並べた時に等比数列をなしており，さらに2つの差が正となるように差を求め，その差を小さい順に並べると等差数列となっている．最も小さい値を\(a\)としたとき，3つの数を求めよ．

数列

問題：\(a_{n}>0\)を条件とする．\(S_{n}=\displaystyle \sum_{k=1}^{n}a_{k}\)として，\(a_{n}^{2}+\displaystyle \frac{1}{4}n=S_{n}\)\((n\geqq 1)\)が成り立つとき，\(a_{n}\)を求めよ．